Problema 1: Examen de 2025 de Andalucía
-
Una viga rígida, considerada como un objeto unidimensional, debe ser transportada horizontalmente a ras de suelo a través de un pasillo que gira en ángulo recto.
La anchura del pasillo antes de la esquina es
𝑎 𝑏 -
A la gran final de un torneo de ajedrez han llegado Alicia y Berta.
En este deporte, la victoria otorga un punto y las tablas medio punto.
Para saber quién será la campeona final, van a jugar dos partidas y ganará aquella que obtenga mayor puntuación.
En caso de empate, se repetirá el proceso.
Se sabe que, en una partida,
𝑝 𝑞 𝑟 𝑟 = 𝑞 = 0 , 2 5 - Demostrar que el producto de los catetos de un triángulo rectángulo donde todos los lados son números naturales es múltiplo de 12.
Resolución
-
Sean
𝑙 𝑂 𝑂 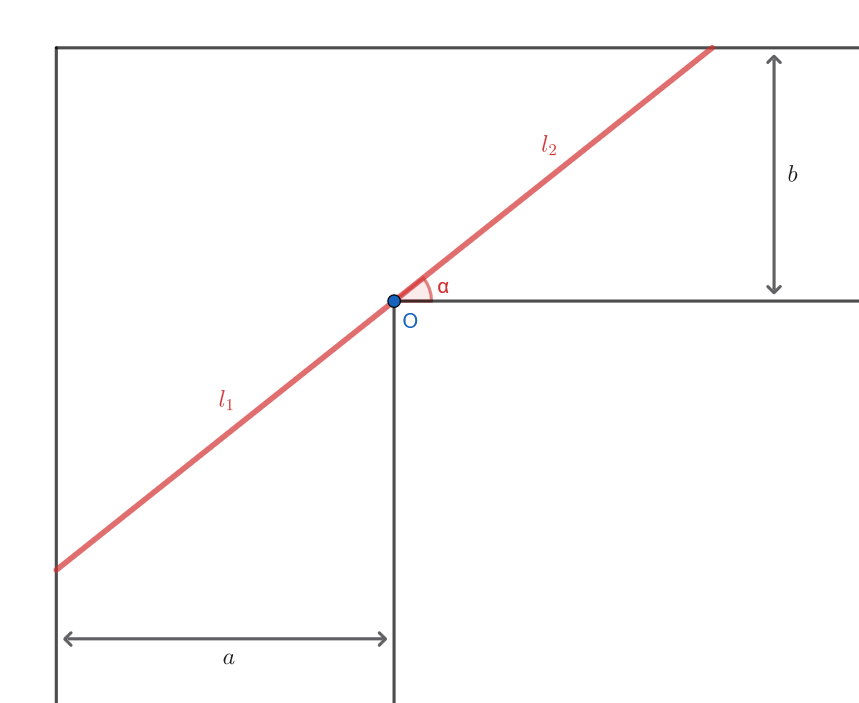 Sea
Sea 𝛼 ∈ ( 0 , 𝜋 2 ) 𝑙 1 𝑙 2 𝑂 c o s ( 𝛼 ) = 𝑎 𝑙 1 ⇒ 𝑙 1 = 𝑎 c o s ( 𝛼 ) , s e n ( 𝛼 ) = 𝑏 𝑙 2 ⇒ 𝑙 2 = 𝑏 s e n ( 𝛼 ) . 𝛼 𝑙 = 𝑙 1 + 𝑙 2 = 𝑎 c o s ( 𝛼 ) + 𝑏 s e n ( 𝛼 ) . 𝑓 ( 𝛼 ) = 𝑎 c o s ( 𝛼 ) + 𝑏 s e n ( 𝛼 ) . 𝑓 ′ ( 𝛼 ) = − 𝑎 c o s 2 ( 𝛼 ) ⋅ ( − s e n ( 𝛼 ) ) − 𝑏 s e n 2 ( 𝛼 ) ⋅ c o s ( 𝛼 ) = 𝑎 s e n ( 𝛼 ) c o s 2 ( 𝛼 ) − 𝑏 c o s ( 𝛼 ) s e n 2 ( 𝛼 ) . 𝑓 ′ ( 𝛼 ) = 0 ⇔ 𝑎 s e n ( 𝛼 ) c o s 2 ( 𝛼 ) − 𝑏 c o s ( 𝛼 ) s e n 2 ( 𝛼 ) = 0 ⇔ 𝑎 s e n ( 𝛼 ) c o s 2 ( 𝛼 ) = 𝑏 c o s ( 𝛼 ) s e n 2 ( 𝛼 ) ⇔ 𝑎 s e n 3 ( 𝛼 ) = 𝑏 c o s 3 ( 𝛼 ) ⇔ t g 3 ( 𝛼 ) = 𝑏 𝑎 ⇔ ⇔ t g ( 𝛼 ) = 3 √ 𝑏 𝑎 ⇔ 𝛼 = a r c t g ( 3 √ 𝑏 𝑎 ) . 𝛼 = a r c t g ( 3 √ 𝑏 𝑎 ) l í m 𝛼 → 0 + 𝑓 ′ ( 𝛼 ) = l í m 𝛼 → 0 + ( 𝑎 s e n ( 𝛼 ) c o s 2 ( 𝛼 ) − 𝑏 c o s ( 𝛼 ) s e n 2 ( 𝛼 ) ) = − ∞ , l í m 𝛼 → 𝜋 2 − 𝑓 ′ ( 𝛼 ) = l í m 𝛼 → 𝜋 2 − ( 𝑎 s e n ( 𝛼 ) c o s 2 ( 𝛼 ) − 𝑏 c o s ( 𝛼 ) s e n 2 ( 𝛼 ) ) = + ∞ . Así que el mínimo absoluto de la función se alcanza en( 0 , a r c t g ( 3 √ 𝑏 𝑎 ) ) ( a r c t g ( 3 √ 𝑏 𝑎 ) , 𝜋 2 ) signo de 𝑓 ′ − + monotonía de 𝑓 → → 𝛼 = a r c t g ( 3 √ 𝑏 𝑎 ) 𝑙 = 𝑎 c o s ( 𝛼 0 ) + 𝑏 s e n ( 𝛼 0 ) , c o n 𝛼 0 = a r c t g ( 3 √ 𝑏 𝑎 ) . t g ( 𝛼 ) = s e n ( 𝛼 ) c o s ( 𝛼 ) ⇒ t g 2 ( 𝛼 ) = s e n 2 ( 𝛼 ) ⋅ 1 c o s 2 ( 𝛼 ) = s e n 2 ( 𝛼 ) ( 1 + t g 2 ( 𝛼 ) ) ⇔ s e n 2 ( 𝛼 ) = t g 2 ( 𝛼 ) 1 + t g 2 ( 𝛼 ) , c o s 2 ( 𝛼 ) = 1 − s e n 2 ( 𝛼 ) = 1 − t g 2 ( 𝛼 ) 1 + t g 2 ( 𝛼 ) = 1 1 + t g 2 ( 𝛼 ) . 𝑙 = 𝑎 √ 1 + t g 2 ( 𝛼 0 ) + 𝑏 √ 1 + t g 2 ( 𝛼 0 ) t g ( 𝛼 0 ) = ( 𝑎 + 𝑏 t g ( 𝛼 0 ) ) √ 1 + t g 2 ( 𝛼 0 ) = ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ 𝑎 + 𝑏 3 √ 𝑏 𝑎 ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ √ √ √ √ √ ⎷ 1 + ( 3 √ 𝑏 𝑎 ) 2 = = ( 𝑎 + 𝑏 3 √ 𝑎 3 √ 𝑏 ) √ √ √ √ √ ⎷ 1 + ( 3 √ 𝑏 𝑎 ) 2 = ( 𝑎 + 𝑎 1 3 ⋅ 𝑏 2 3 ) √ 1 + ( 𝑏 𝑎 ) 2 3 = 3 √ 𝑎 ( 𝑎 2 3 + 𝑏 2 3 ) √ 1 + ( 𝑏 𝑎 ) 2 3 . -
Sean los sucesos:
𝐴 = 𝐴 𝑙 𝑖 𝑐 𝑖 𝑎 𝑔 𝑎 𝑛 𝑎 𝑙 𝑎 𝑝 𝑎 𝑟 𝑡 𝑖 𝑑 𝑎 , 𝐵 = 𝐵 𝑒 𝑟 𝑡 𝑎 𝑔 𝑎 𝑛 𝑎 𝑙 𝑎 𝑝 𝑎 𝑟 𝑡 𝑖 𝑑 𝑎 , 𝑇 = 𝑙 𝑎 𝑝 𝑎 𝑟 𝑡 𝑖 𝑑 𝑎 𝑡 𝑒 𝑟 𝑚 𝑖 𝑛 𝑎 𝑒 𝑛 𝑡 𝑎 𝑏 𝑙 𝑎 𝑠 , 𝑅 𝐴 = 𝐴 𝑙 𝑖 𝑐 𝑖 𝑎 𝑔 𝑎 𝑛 𝑎 𝑙 𝑎 𝑟 𝑜 𝑛 𝑑 𝑎 , 𝑅 𝐵 = 𝐵 𝑒 𝑟 𝑡 𝑎 𝑔 𝑎 𝑛 𝑎 𝑙 𝑎 𝑟 𝑜 𝑛 𝑑 𝑎 , 𝑅 𝐸 = 𝑙 𝑎 𝑟 𝑜 𝑛 𝑑 𝑎 𝑞 𝑢 𝑒 𝑑 𝑎 𝑒 𝑛 𝑒 𝑚 𝑝 𝑎 𝑡 𝑒 , 𝐺 𝐴 = 𝐴 𝑙 𝑖 𝑐 𝑖 𝑎 𝑔 𝑎 𝑛 𝑎 𝑒 𝑙 𝑡 𝑜 𝑟 𝑛 𝑒 𝑜 , 𝐺 𝐵 = 𝐵 𝑒 𝑟 𝑡 𝑎 𝑔 𝑎 𝑛 𝑎 𝑒 𝑙 𝑡 𝑜 𝑟 𝑛 𝑒 𝑜 . Las probabilidades de obtener los distintos resultados al terminar la ronda de dos partidas son:𝐴 ( 2 − 0 ) 𝑝 ←←←←←←←←← → 𝐴 𝑞 ←←←←←←←←← → 𝐵 ( 1 − 1 ) 𝑝 ←←←←←←←←← → 𝑟 ←←←←←←←←← → 𝑇 ( 1 , 5 − 0 , 5 ) 𝐴 ( 1 − 1 ) 𝑝 ←←←←←←←←← → 𝑞 ←←←←←←←←← → 𝐵 𝑞 ←←←←←←←←← → 𝐵 ( 0 − 2 ) 𝑟 ←←←←←←←←← → 𝑇 ( 0 , 5 − 1 , 5 ) 𝐴 ( 1 , 5 − 0 , 5 ) 𝑟 ←←←←←←←←← → 𝑝 ←←←←←←←←← → 𝑇 𝑞 ←←←←←←←←← → 𝐵 ( 0 , 5 − 1 , 5 ) 𝑟 ←←←←←←←←← → 𝑇 ( 1 − 1 ) 𝑃 ( 𝑅 𝐴 ) = 𝑃 ( 𝐴 ∩ 𝐴 ) + 𝑃 ( 𝐴 ∩ 𝑇 ) + 𝑃 ( 𝑇 ∩ 𝐴 ) = 𝑃 ( 𝐴 ) ⋅ 𝑃 ( 𝐴 | 𝐴 ) + 𝑃 ( 𝐴 ) ⋅ 𝑃 ( 𝑇 | 𝐴 ) + 𝑃 ( 𝑇 ) ⋅ 𝑃 ( 𝐴 | 𝑇 ) = = 𝑝 2 + 𝑝 𝑟 + 𝑟 𝑝 = 𝑝 2 + 2 𝑝 𝑟 = 𝑝 ( 𝑝 + 2 𝑟 ) , 𝑃 ( 𝑅 𝐵 ) = 𝑃 ( 𝐵 ∩ 𝐵 ) + 𝑃 ( 𝐵 ∩ 𝑇 ) + 𝑃 ( 𝑇 ∩ 𝐵 ) = 𝑃 ( 𝐵 ) ⋅ 𝑃 ( 𝐵 | 𝐵 ) + 𝑃 ( 𝐵 ) ⋅ 𝑃 ( 𝑇 | 𝐵 ) + 𝑃 ( 𝑇 ) ⋅ 𝑃 ( 𝐵 | 𝑇 ) = = 𝑞 2 + 𝑞 𝑟 + 𝑟 𝑞 = 𝑞 2 + 2 𝑞 𝑟 = 𝑞 ( 𝑞 + 2 𝑟 ) , 𝑃 ( 𝑅 𝐸 ) = 𝑃 ( 𝐴 ∩ 𝐵 ) + 𝑃 ( 𝐵 ∩ 𝐴 ) + 𝑃 ( 𝑇 ∩ 𝑇 ) = 𝑃 ( 𝐴 ) ⋅ 𝑃 ( 𝐵 | 𝐴 ) + 𝑃 ( 𝐵 ) ⋅ 𝑃 ( 𝐴 | 𝐵 ) + 𝑃 ( 𝑇 ) ⋅ 𝑃 ( 𝑇 | 𝑇 ) = = 𝑝 𝑞 + 𝑞 𝑟 + 𝑟 2 = 𝑟 2 + 2 𝑝 𝑞 . 𝑃 ( 𝐺 𝐴 ) = 𝑃 ( 𝑅 𝐴 ) + 𝑃 ( 𝑅 𝐸 ) ⋅ 𝑃 ( 𝑅 𝐴 ) + 𝑃 ( 𝑅 𝐸 ) 2 ⋅ 𝑃 ( 𝑅 𝐴 ) + … = ∞ ∑ 𝑛 = 0 𝑃 ( 𝑅 𝐴 ) ⋅ 𝑃 ( 𝑅 𝐸 ) 𝑛 = 𝑃 ( 𝑅 𝐴 ) ⋅ ∞ ∑ 𝑛 = 0 ( 𝑟 2 + 2 𝑝 𝑞 ) 𝑛 , 𝑃 ( 𝐺 𝐵 ) = 𝑃 ( 𝑅 𝐵 ) + 𝑃 ( 𝑅 𝐸 ) ⋅ 𝑃 ( 𝑅 𝐵 ) + 𝑃 ( 𝑅 𝐸 ) 2 ⋅ 𝑃 ( 𝑅 𝐵 ) + … = ∞ ∑ 𝑛 = 0 𝑃 ( 𝑅 𝐵 ) ⋅ 𝑃 ( 𝑅 𝐸 ) 𝑛 = 𝑃 ( 𝑅 𝐵 ) ⋅ ∞ ∑ 𝑛 = 0 ( 𝑟 2 + 2 𝑝 𝑞 ) 𝑛 . 𝑝 + 𝑞 + 𝑟 = 1 ⇒ ( 𝑝 + 𝑞 + 𝑟 ) 2 = 1 ⇔ 1 = 𝑝 2 + 𝑞 2 + 𝑟 2 + 2 𝑝 𝑞 + 2 𝑝 𝑟 + 2 𝑞 𝑟 > 𝑟 2 + 2 𝑝 𝑞 > 0 . | 𝑟 2 + 2 𝑝 𝑞 | < 1 ∞ ∑ 𝑛 = 0 ( 𝑟 2 + 2 𝑝 𝑞 ) 𝑛 = 1 1 − 𝑟 2 − 2 𝑝 𝑞 . 𝑃 ( 𝐺 𝐴 ) = 𝑃 ( 𝑅 𝐴 ) ⋅ ∞ ∑ 𝑛 = 0 ( 𝑟 2 + 2 𝑝 𝑞 ) 𝑛 = 𝑝 ( 𝑝 + 2 𝑟 ) 1 − 𝑟 2 − 2 𝑝 𝑞 , 𝑃 ( 𝐺 𝐵 ) = 𝑃 ( 𝑅 𝐵 ) ⋅ ∞ ∑ 𝑛 = 0 ( 𝑟 2 + 2 𝑝 𝑞 ) 𝑛 = 𝑞 ( 𝑞 + 2 𝑟 ) 1 − 𝑟 2 − 2 𝑝 𝑞 . 𝑞 = 𝑟 = 0 , 2 5 𝑝 = 0 , 5 𝑃 ( 𝐺 𝐴 ) = 0 , 5 ( 0 , 5 + 2 ⋅ 0 , 2 5 ) 1 − 0 , 2 5 2 − 2 ⋅ 0 , 5 ⋅ 0 , 2 5 = 8 1 1 , 𝑃 ( 𝐺 𝐵 ) = 0 , 2 5 ( 0 , 2 5 + 2 ⋅ 0 , 2 5 ) 1 − 0 , 2 5 2 − 2 ⋅ 0 , 5 ⋅ 0 , 2 5 = 3 1 1 . -
Sean
𝑎 𝑏 𝑐 𝑎 𝑏 𝑐 𝑎 𝑏 𝑐 Todas las ternas pitagóricas primitivas son de la forma:
⎧ { { ⎨ { { ⎩ 𝑎 = 𝑚 2 − 𝑛 2 , 𝑏 = 2 𝑚 𝑛 , 𝑐 = 𝑚 2 + 𝑛 2 , c o n 𝑚 , 𝑛 ∈ ℕ y 𝑛 < 𝑚 . 𝑚 𝑛 𝑎 𝑏 𝑐 𝑚 𝑛 El producto de los catetos viene dado por:
𝑎 𝑏 = 2 𝑚 𝑛 ( 𝑚 2 − 𝑛 2 ) = 2 𝑚 𝑛 ( 𝑚 − 𝑛 ) ( 𝑚 + 𝑛 ) . 𝑚 𝑛 𝑎 𝑏 𝑎 𝑏 -
Si
𝑚 𝑛 𝑎 𝑏 -
Si
𝑚 𝑛 𝑚 = 3 𝑘 + 1 o b i e n 𝑚 = 3 𝑘 + 2 , c o n 𝑘 ∈ ℕ ∪ { 0 } , 𝑛 = 3 𝑞 + 1 o b i e n 𝑛 = 3 𝑞 + 2 , c o n 𝑞 ∈ ℕ ∪ { 0 } . -
Supongamos que:
{ 𝑚 = 3 𝑘 + 1 , 𝑛 = 3 𝑞 + 1 o b i e n { 𝑚 = 3 𝑘 + 2 , 𝑛 = 3 𝑞 + 2 . 𝑚 − 𝑛 = 3 𝑘 − 3 𝑞 = 3 ( 𝑘 − 𝑞 ) . 𝑚 − 𝑛 𝑎 𝑏 -
Supongamos que:
{ 𝑚 = 3 𝑘 + 1 , 𝑛 = 3 𝑞 + 2 o b i e n { 𝑚 = 3 𝑘 + 2 , 𝑛 = 3 𝑞 + 1 . 𝑚 + 𝑛 = 3 𝑘 + 3 𝑞 + 3 = 3 ( 𝑘 + 𝑞 + 1 ) . 𝑚 + 𝑛 𝑎 𝑏
-
Supongamos que:
Como el producto
𝑎 𝑏 -
Si
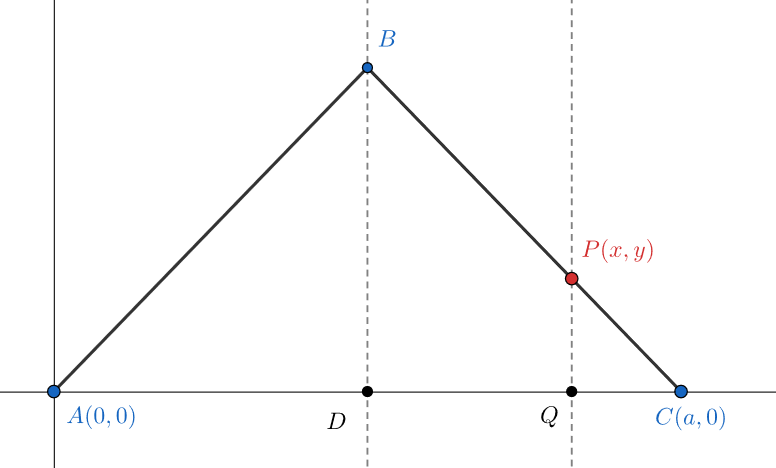 Sea
Sea 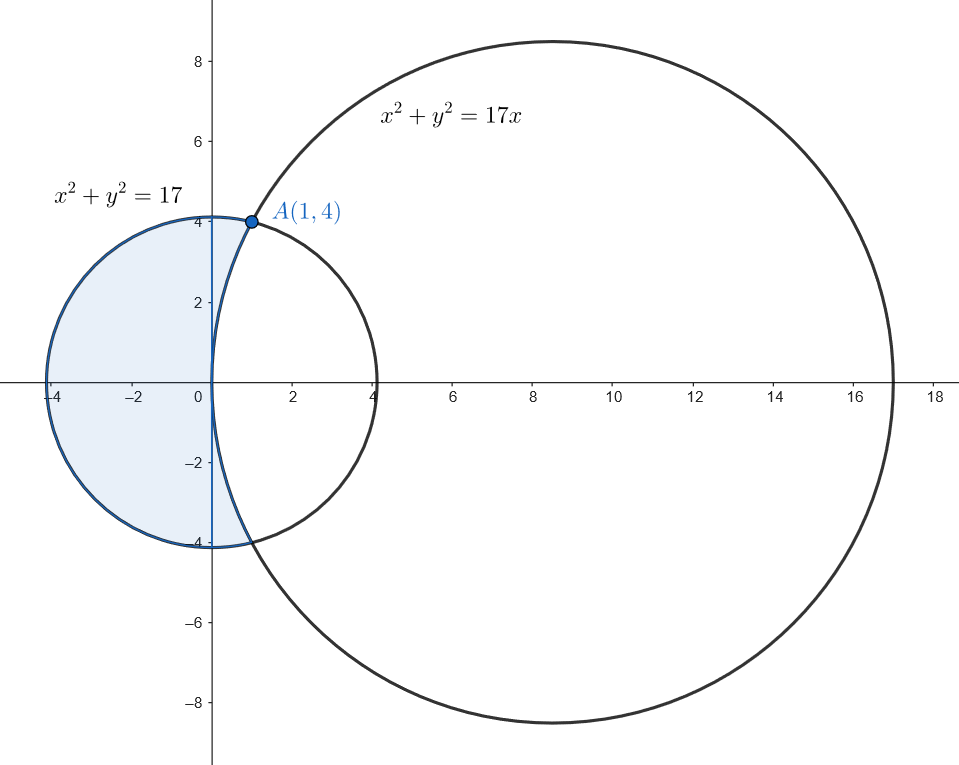 Podemos dividir esta región en dos partes que en conjunto generan el mismo sólido al girar alrededor del eje.
Podemos dividir esta región en dos partes que en conjunto generan el mismo sólido al girar alrededor del eje.
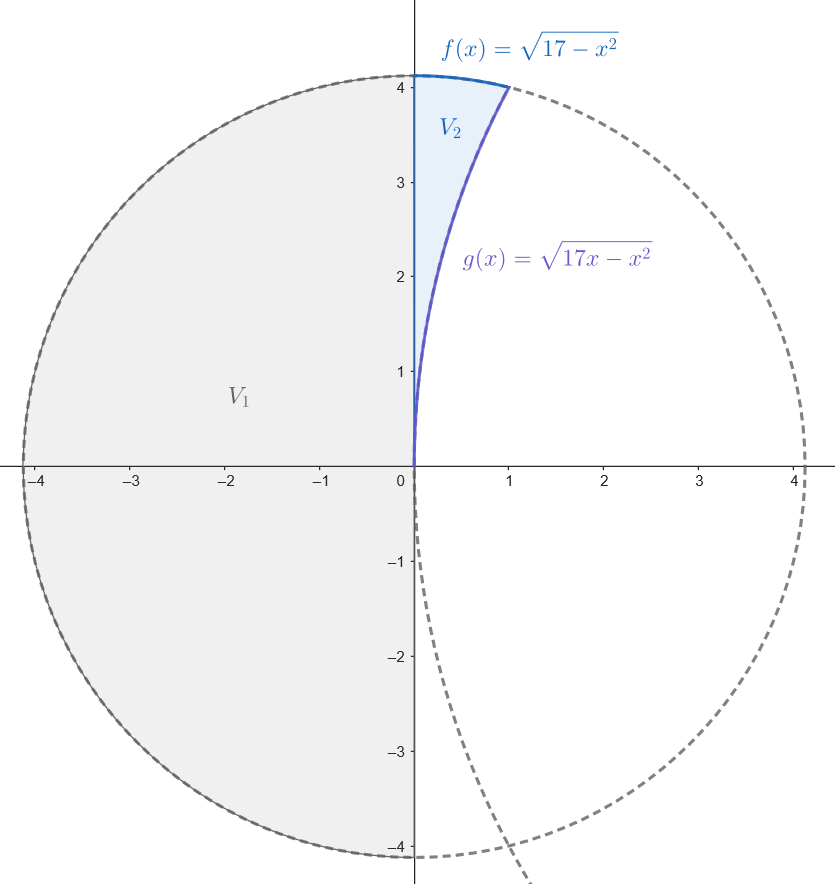
 El volumen del sólido generado al girar esta región será la diferencia de los volúmenes generados por las regiones descritas por las funciones
El volumen del sólido generado al girar esta región será la diferencia de los volúmenes generados por las regiones descritas por las funciones 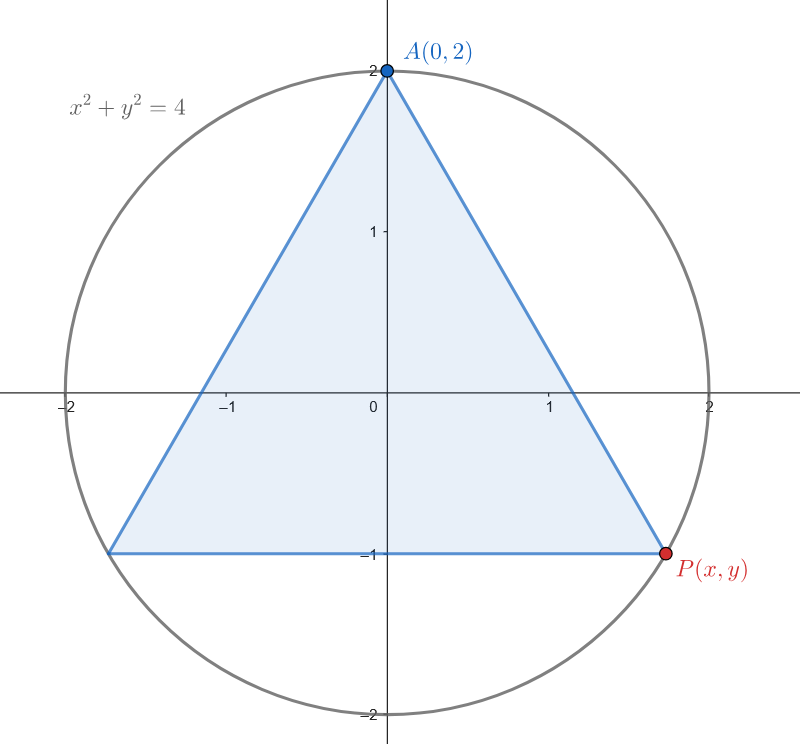 Observamos que la base del triángulo es
Observamos que la base del triángulo es 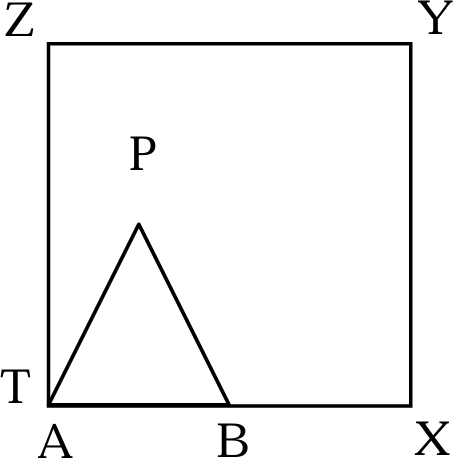
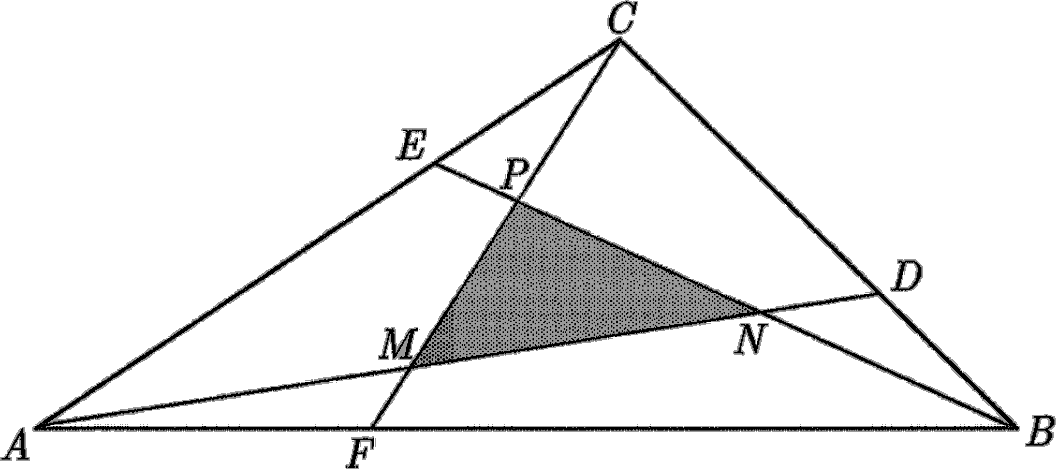
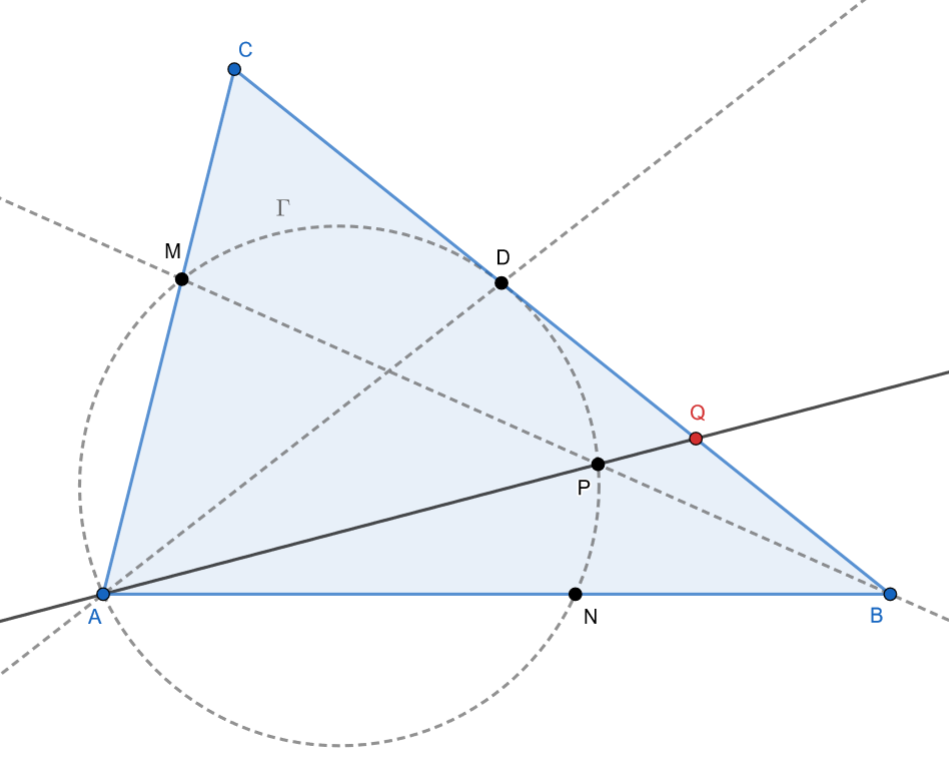
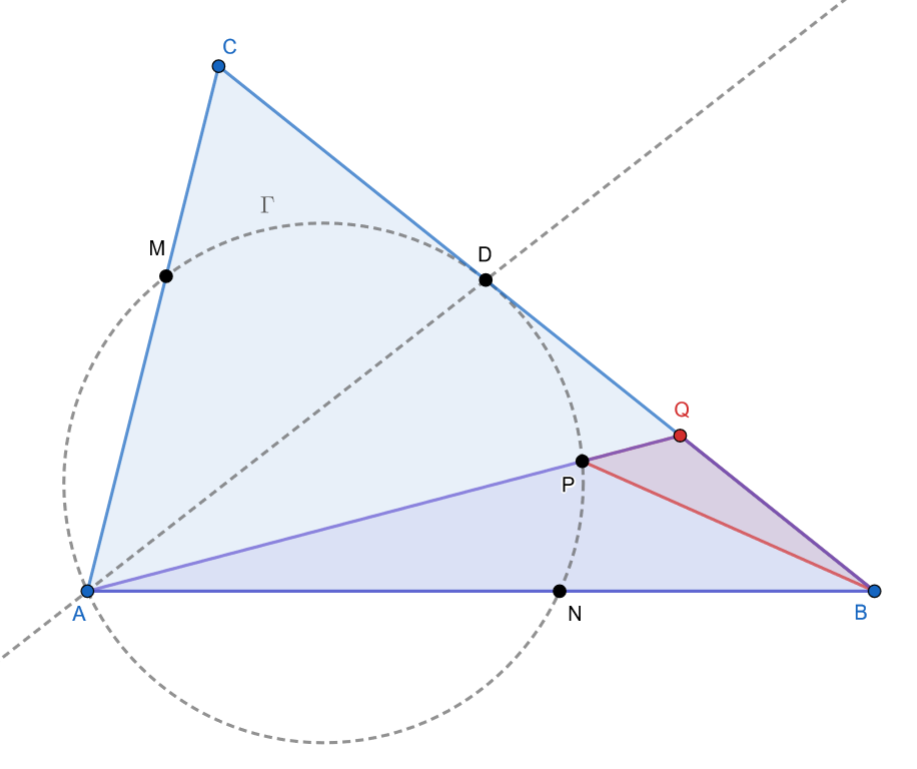
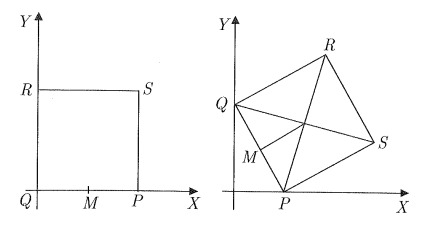 Con las notaciones de la figura, en las que se muestran la posición inicial del cuadrado y una de las posiciones intermedias, determinar el lugar geométrico descrito por los siguientes puntos:
Con las notaciones de la figura, en las que se muestran la posición inicial del cuadrado y una de las posiciones intermedias, determinar el lugar geométrico descrito por los siguientes puntos:
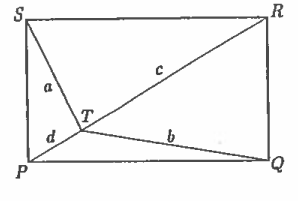 Demuestre que:
Demuestre que: