Icono Matemáticas de oposiciones

GitHub

📋 Examen de 2015 de Castilla la Mancha

Problema 1

Sea 𝑅 la región del plano delimitada por los semiejes positivos de coordenadas y la curva 𝑦 =2cos⁡(𝑥), entre 𝑥 =0 y 𝑥 =𝜋2. Halle el valor de 𝑎 ∈ℝ para que la curva 𝑦 =𝑎sen⁡(𝑥) divida a 𝑅 en dos regiones de igual área.

Resolución

Hallamos el punto de corte de las dos curvas en el intervalo (0,𝜋2). 2cos⁡(𝑥)=𝑎sen⁡(𝑥)⇔tg⁡(𝑥)=2𝑎⇔𝑥=arctg⁡(2𝑎).

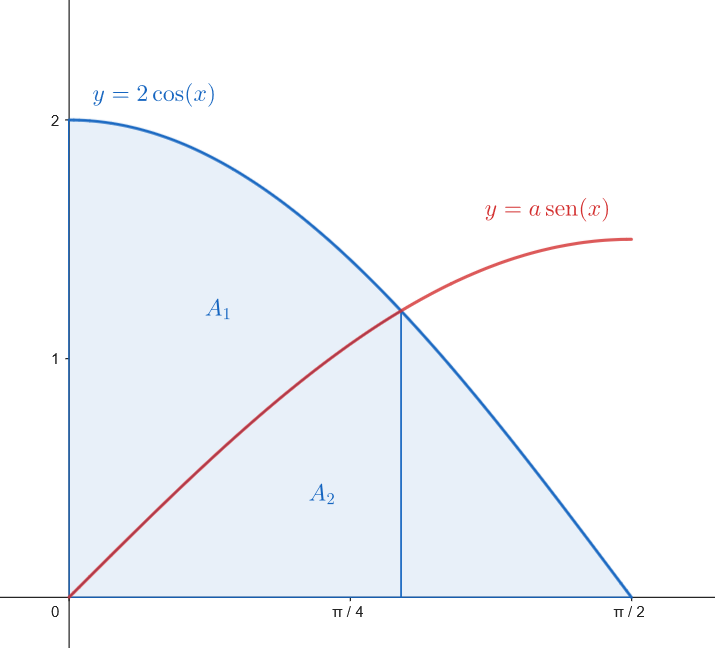
Realizamos un esbozo de las dos curvas. Figura

Llamamos 𝐴1 al área de la región superior, 𝐴2 al de la región inferior y 𝐴 al de la región completa, con 𝐴 =𝐴1 +𝐴2. Ha de verificarse que 𝐴1 =𝐴2 o, equivalentemente, 𝐴1 =𝐴2. Hallamos estas áreas. 𝐴=∫𝜋202cos⁡(𝑥)𝑑𝑥=2[sen⁡(𝑥)]𝜋20=2𝑢2,𝐴1=∫arctg⁡(2𝑎)0(2cos⁡(𝑥)−𝑎sen⁡(𝑥))𝑑𝑥=[2sen⁡(𝑥)+𝑎cos⁡(𝑥)]arctg⁡(2𝑎)0==2sen⁡(arctg⁡(2𝑎))+𝑎cos⁡(arctg⁡(2𝑎))−𝑎

Sea 𝛼 =arctg⁡(2𝑎). Entonces: tg⁡(𝛼)=2𝑎⇒⎧{ { {⎨{ { {⎩sen⁡(𝛼)=2√4+𝑎2,cos⁡(𝛼)=𝑎√4+𝑎2. Luego: 𝐴1=2sen⁡(𝛼)+𝑎cos⁡(𝛼)−𝑎=4√4+𝑎2+𝑎2√4+𝑎2−𝑎=4+𝑎2√4+𝑎2−𝑎=√4+𝑎2−𝑎.

Por tanto, 𝐴1=𝐴2⇔𝐴1=𝐴2⇔√4+𝑎2−𝑎=1⇔4+𝑎2=𝑎2+2𝑎+1⇔2𝑎=3⇔𝑎=32.

Problema 2

Demuestre la veracidad o falsedad del siguiente enunciado: Para todo 𝑛 ∈ℕ se puede encontrar un conjunto de 𝑛 números naturales consecutivos que no contiene a ningún número primo.

Problema 3

En el triángulo acutángulo 𝐴𝐵𝐶 se consideran los puntos 𝐻, 𝐷 y 𝑀 del lado 𝐵𝐶, que son pies respectivos de la altura 𝐴𝐻, de la bisectriz 𝐴𝐷 y de la mediana 𝐴𝑀 que parten desde 𝐴. Si las longitudes de 𝐴𝐵, 𝐴𝐶 y 𝑀𝐷 son, respectivamente, 11, 8 y 1, calcule la longitud del segmento 𝐷𝐻.