Icono Matemáticas de oposiciones

GitHub

📋 Examen de 2018 de Islas Baleares

Problema 1

Demuestre que si 𝑛 es un número entero impar, entonces el residuo de la división entera de 𝑛2 entre 8 es 1.

Problema 2

Encuentre todos los números enteros 𝑏 y 𝑐 que hacen que la ecuación 𝑥2 +𝑏𝑥 +𝑐 =0 tenga dos soluciones diferentes y reales, 𝛼 y 𝛽, y tales que 𝛼2 +𝛽2 =5.

Resolución

Sean 𝛼 y 𝛽 las dos soluciones de la ecuación, tales que 𝛼2 +𝛽2 =5. Por las relaciones de Cardano-Vietta, se tiene que: {𝛼𝛽=𝑐,𝛼+𝛽=−𝑏. Completando cuadrados, obtenemos que: 𝛼2+𝛽2=(𝛼+𝛽)2−2𝛼𝛽=𝑏2−2𝑐. De esta forma, se tiene que: 𝛼2+𝛽2=5⇔𝑏2−2𝑐=5⇔𝑏2=5+2𝑐. En primer lugar, observamos que: 𝑏2≥0⇔5+2𝑐≥0⇔2𝑐≥−5⇔𝑐≥−52𝑐∈ℤ⇔𝑐≥−2. Por otro lado, para que la ecuación tenga dos soluciones reales y distintas ha de verificarse: 𝑏2−4𝑐>0⇔5−2𝑐>0⇔2𝑐<5⇔𝑐<52𝑐∈ℤ⇔𝑐≤2. Luego −2 ≤𝑐 ≤2.

  • Si 𝑐 = −2, entonces 𝑏2 =1. Así que 𝑏 = ±1.
  • Si 𝑐 = −1, entonces 𝑏2 =3. Como 𝑏 ∉ℤ, esta posibilidad no es válida.
  • Si 𝑐 =0, entonces 𝑏2 =5. Como 𝑏 ∉ℤ, esta posibilidad no es válida.
  • Si 𝑐 =1, entonces 𝑏2 =7. Como 𝑏 ∉ℤ, esta posibilidad no es válida.
  • Si 𝑐 =2, entonces 𝑏2 =9. Así que 𝑏 = ±3.

Por tanto, los posibles valores de 𝑏 y 𝑐 son: {𝑏=−1,𝑐=−2,{𝑏=1,𝑐=−2,{𝑏=−3,𝑐=2,{𝑏=3,𝑐=2.

Problema 3

Sea 𝑓 :[0,1] →(0,1) una función continua. Demuestre que la ecuación 2𝑥−∫𝑥0𝑓(𝑡)𝑑𝑡=1 tiene una única solución real.

Resolución

Sea 𝑔 :[0,1] →ℝ la función dada por: 𝑔(𝑥)=2𝑥−1−∫𝑥0𝑓(𝑡)𝑑𝑡. Dado que 𝑓 es continua, por el teorema fundamental del cálculo se tiene que la función 𝑔 es derivable con: 𝑔′(𝑥)=2−𝑓(𝑥),𝑥∈(0,1). Como por hipótesis sabemos que 0 <𝑓(𝑥) <1 para todo 𝑥 ∈[0,1], entonces 𝑔′(𝑥) >0 para todo 𝑥 ∈(0,1). Así que 𝑔 es estrictamente creciente en (0,1) y, en consecuencia, alcanza su mínimo en 𝑥 =0 y su máximo en 𝑥 =1.

Hallamos el valor de 𝑔 en sus extremos. 𝑔(0)=−1,𝑔(1)=1−∫10𝑓(𝑡)𝑑𝑡. De nuevo, como 0 <𝑓(𝑥) <1 para todo 𝑥 ∈[0,1], entonces: 0≤∫10𝑓(𝑡)𝑑𝑡≤∫101𝑑𝑡=1. Así que: 𝑔(1)=1−∫10𝑓(𝑡)𝑑𝑡≥1−1=0.

Dado que 𝑔(0) <0, 𝑔(1) ≥0 y 𝑔 es continua en [0,1], por el teorema de Bolzano se tiene que existe 𝑐 ∈[0,1] tal que 𝑔(𝑐) =0, esto es, tal que 𝑐 es solución de la ecuación. Como además 𝑔 es estrictamente creciente en (0,1), dicho número 𝑐 es único. Por tanto, la ecuación tiene una única solución real.

Problema 4

Un cuadrado de vértices 𝐴, 𝐵, 𝐶 y 𝐷 de centro 𝑂 y lado 1 gira un ángulo 𝛼 alrededor del punto 𝑂. Encuentre el área común a ambos cuadrados.

Problema 5

La función de densidad de una variable aleatoria continua 𝑋 es 𝑓(𝑥)={𝑘𝑒−𝑥/2,si 𝑥>0,0,si −∞<𝑥≤0.

  1. Calcule el valor del parámetro 𝑘.
  2. Encuentre la esperanza matemática de 𝑋.

Resolución
  1. Observamos que: ∫ℝ𝑓(𝑥)𝑑𝑥=∫+∞0𝑘𝑒−𝑥/2𝑑𝑥=−2𝑘[𝑒−𝑥/2]+∞0=2𝑘. Como 𝑓 es una función de densidad, ha de verificarse que: ∫ℝ𝑓(𝑥)𝑑𝑥=1⇔2𝑘=1⇔𝑘=12.
  2. La esperanza de 𝑋 viene dada por: 𝐸(𝑋)=∫ℝ𝑥𝑓(𝑥)𝑑𝑥=∫∞012𝑥𝑒−𝑥/2𝑑𝑥. Integramos por partes. 𝑢=𝑥⇒𝑢′=1,𝑣′=12𝑒−𝑥/2⇒𝑣=−𝑒−𝑥/2. Por tanto, 𝐸(𝑋)=∫∞012𝑥𝑒−𝑥/2𝑑𝑥=[−𝑥𝑒−𝑥/2]+∞0+∫+∞0𝑒−𝑥/2=2.

Problema 6

Encuentre un número natural 𝑛 de tal manera que el número 25 ⋅18𝑛 tenga 348 divisores más que el número 72.

Resolución

Sea 𝑚 =25 ⋅18𝑛 =2𝑛 ⋅32𝑛 ⋅52. Observamos en primer lugar que el número 72 tiene 4 ⋅3 =12 divisores, así que 𝑚 ha de tener 360 divisores.

El número 𝑚 tiene (𝑛 +1) ⋅(2𝑛 +1) ⋅3 divisores. Para que tenga 360 divisores, ha de verificarse: 3(𝑛+1)(2𝑛+1)=360⇔2𝑛2+3𝑛+1=120⇔2𝑛2+3𝑛−119=0⇔{𝑛=−172∉ℕ,𝑛=7. Por tanto, 𝑛 =7.

Problema 7

Resuelva la ecuación ∣ ∣ ∣ ∣ ∣𝑥33𝑥23𝑥1𝑥2𝑥2+2𝑥2𝑥+11𝑥2𝑥+1𝑥+211331∣ ∣ ∣ ∣ ∣=0.

Problema 8

Calcule el siguiente límite: lím𝑛→∞⁡∫2𝜋0sen⁡(𝑛𝑥)𝑥2+𝑛2𝑑𝑥.

Problema 9

Sean △𝐴𝐵𝐶 un triángulo, 𝛽 =∠𝐴𝐵𝐶 y 𝛾 =∠𝐴𝐶𝐵. Se denotan las longitudes de los lados mediante 𝑎 =𝐵𝐶, 𝑏 =𝐴𝐶 y 𝑐 =𝐴𝐵. Pruebe que si 𝛾 =2𝛽 entonces 𝑐2 =(𝑎 +𝑏)𝑏.

Problema 10

Dado un segmento, se escogen dos puntos al azar que lo dividen en tres partes. ¿Cuál es la probabilidad de que se pueda construir un triángulo con esas tres partes?

Resolución

Supongamos sin pérdida de generalidad que el segmento es de longitud 1. Sea 𝑥 la longitud de la primera parte y sea 𝑦 la longitud de la segunda parte. Figura

La región factible es el conjunto: Ω={(𝑥,𝑦)∈ℝ2:0<𝑥<1,0<𝑦<1,𝑥+𝑦<1}.

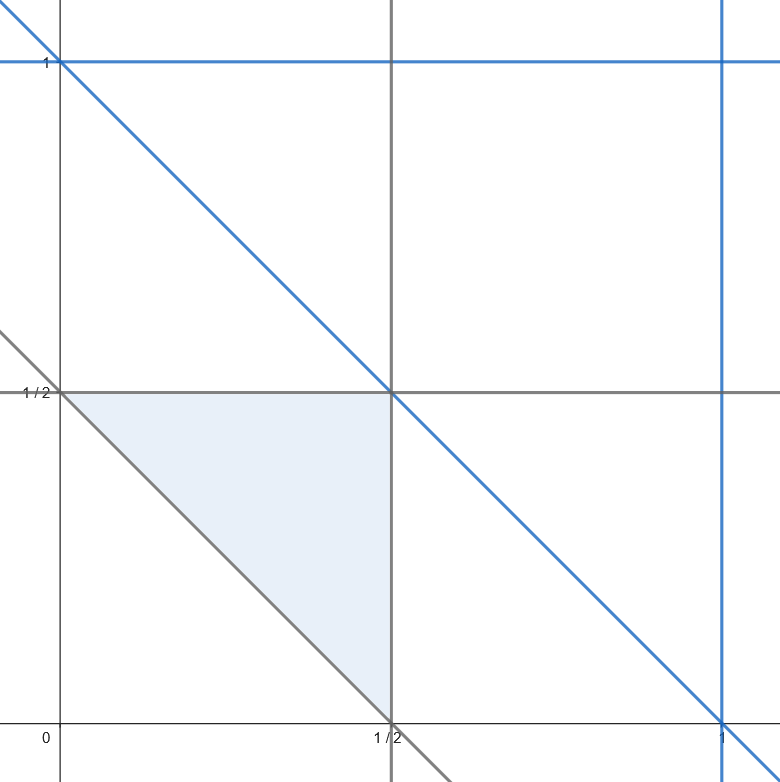
Para que se pueda construir un triángulo, es necesario que la longitud de cada lado sea menor que la suma de los otros dos. Así que se tienen que verificar las siguientes condiciones: ⎧{ {⎨{ {⎩𝑥<𝑦+1−𝑥−𝑦,𝑦<𝑥+1−𝑥−𝑦,1−𝑥−𝑦<𝑥+𝑦⇔⎧{ {⎨{ {⎩𝑥<12,𝑦<12,2𝑥+2𝑦>1. Representamos la región favorable. Figura

Observamos que el área de la región favorable es: 𝑆𝐹=12⋅122=18𝑢2. Además, el área de la región factible es 𝑆Ω =12 𝑢2. Por tanto, la probabilidad de que se pueda construir un triángulo con las tres partes es: 𝑝=𝑆𝐹𝑆Ω=1812=14.

Problema 11

Sean 𝑃3 el espacio vectorial de los polinomios en la variable 𝑥 de grado menor o igual que tres, y 𝑃2 el espacio vectorial de los polinomios en la variable 𝑥 de grado menor o igual que dos. Se considera la aplicación 𝑓:𝑃3→𝑃2,𝑎𝑥3+𝑏𝑥2+𝑐𝑥+𝑑↦3𝑎𝑥2+2𝑏𝑥+𝑐.

  1. Comprobar que 𝑓 es homomorfismo.
  2. Clasificar el homomorfismo.

Problema 12

Calcule la siguiente integral 𝐼=∫𝑥3−𝑥2+2𝑥𝑥4+𝑥2+1𝑑𝑥.

Problema 13

Hallar todas las cuaternas 𝑢 =(𝑥,𝑦,𝑧,𝑡) ∈ℝ4 tales que la suma de cualquiera de sus coordenadas con el producto de las tres restantes valga 2.

Problema 14

La curva C, intersección de la esfera 𝑆={(𝑥,𝑦,𝑧)∈ℝ3:𝑥2+𝑦2+𝑧2−2𝑥−2𝑦−4𝑧−4=0} con el plano 𝜋={(𝑥,𝑦,𝑧)∈ℝ3:𝑥+𝑦−𝑧−1=0}, se proyecta ortogonalmente sobre el plano 𝑂𝑋𝑌.

  1. Determine e identifique cuál es la cónica proyección de C.
  2. Encuentre la ecuación reducida de dicha cónica.

Problema 15

Sea 𝑇 :ℝ3 →ℝ3 la aplicación lineal que cumple las siguientes condiciones (referidas a la base canónica):

  • La restricción de 𝑇 al subespacio vectorial 𝑈={(𝑥,𝑦,𝑧)∈ℝ3:𝑥+𝑦−𝑧=0} es una homotecia de razón 4.
  • 𝑇 transforma el subespacio vectorial 𝑉={(𝑥,𝑦,𝑧)∈ℝ3:2𝑥+4𝑦+3𝑧=0,𝑥+𝑦+𝑧=0} en sí mismo.
  • 𝑇(3,0, −1) =(6, −6,8).
Determinar la matriz de 𝑇 respecto de la base canónica.

Problema 16

Un nadador se encuentra situado en un punto 𝐴 del borde de un estanque circular cuyo radio mide 50 metros, y quiere llegar al punto 𝐵 diametralmente opuesto al punto 𝐴. Nadando alcanza un punto 𝑃 del borde del estanque y, a continuación, se dirige hacia el punto 𝐵 caminando por dicho borde. Si nada 50 metros por minuto y camina 100 metros por minuto, ¿a qué punto 𝑃 debe dirigirse para minimizar el tiempo empleado en su recorrido?

Problema 17

Una urna contiene 𝑁 bolas blancas, dos bolas rojas y una bola negra. Se extraen todas las bolas de una en una sin reemplazamiento. Sea 𝑋 la variable aleatoria que indica el número de la extracción en la que ha salido, por primera vez, una bola roja. Sea 𝐴 el suceso "la bola negra es extraída antes de haber sido extraída alguna de las bolas rojas". Determine:

  1. La función de probabilidad de 𝑋.
  2. El valor esperado, esto es, la media 𝐸[𝑋] de 𝑋.
  3. La función de probabilidad de la variable aleatoria 𝑋|𝐴, esto es, 𝑋 condicionada por 𝐴.
  4. El valor esperado, 𝐸[𝑋|𝐴] de 𝑋|𝐴.

Problema 18

Responda razonadamente a las siguientes cuestiones:

  1. Calcule la integral ∫(𝑥+1)𝑑𝑥𝑥3+2𝑥.
  2. Dadas las funciones continuas 𝑓,𝑔 :[𝑎,𝑏] →ℝ se define su producto como ⟨𝑓,𝑔⟩=∫𝑏𝑎𝑓(𝑡)𝑔(𝑡)𝑑𝑡. Demuestre que se cumplen las siguientes propiedades:
    1. Si 𝑓1, 𝑓2, 𝑔 :[𝑎,𝑏] →ℝ son continuas y 𝛼,𝛽 ∈ℝ, entonces: ⟨𝛼𝑓1+𝛽𝑓2,𝑔⟩=𝛼⟨𝑓1,𝑔⟩+𝛽⟨𝑓2,𝑔⟩.
    2. Si 𝑓, 𝑔 :[𝑎,𝑏] →ℝ son continuas, entonces: ⟨𝑓,𝑔⟩=⟨𝑔,𝑓⟩.
    3. Si 𝑓 :[𝑎,𝑏] →ℝ es continua, se cumple que: ⟨𝑓,𝑓⟩≥0.
    4. Si 𝑓 :[𝑎,𝑏] →ℝ es continua, entonces: ⟨𝑓,𝑓⟩=0 si y sólo si 𝑓=0.

Problema 19

  1. Calcule la integral ∫𝜋/20sen7⁡(𝑥)cos2⁡(𝑥)𝑑𝑥.
  2. Estudie la continuidad, existencia de derivadas parciales, derivadas direccionales y diferenciabilidad en el punto (0,0), de la función 𝑓(𝑥,𝑦)={4𝑥3𝑥2+𝑦2,si (𝑥,𝑦)≠(0,0),0,si (𝑥,𝑦)=(0,0).

Problema 20

Demuestre por inducción que 𝑁(𝑛) =𝑛(𝑛+12)(𝑛 +1) es múltiplo de 3 para cada entero positivo 𝑛.

Problema 21

Responda razonadamente a las siguientes cuestiones:

  1. Calcule el límite de la sucesión 𝑎𝑛=𝑛1+𝑛−12+𝑛−23+⋯+3𝑛−2+2𝑛−1+1𝑛log7⁡𝑛!.
  2. Estudie la convergencia de la serie ∞∑𝑛=1(𝑛√𝑒−1−1𝑛).

Problema 22

Sea (𝐸,⟨ ⋅, ⋅⟩) un espacio euclídeo de dimensión finita 𝑛 >1. Sean 𝜓 y 𝜙 dos automorfismos de 𝐸 que conmutan y tales que:

  • 𝜓 es autoadjunto, es decir, ⟨𝜓(𝑥),𝑦⟩ =⟨𝑥,𝜓(𝑦)⟩ para cualesquiera vectores 𝑥,𝑦 ∈𝐸.
  • ⟨𝜙(𝑥),𝑦⟩ = −⟨𝑥,𝜙(𝑦)⟩ para cualesquiera vectores 𝑥,𝑦 ∈𝐸.
Demostrar que:
  1. Para todo 𝑥 ∈𝐸 los vectores 𝜓(𝑥) y 𝜙(𝑥) son ortogonales.
  2. Los endomorfismos 𝜓 +𝜙 y 𝜓 −𝜙 son automorfismos de 𝐸.
  3. Sea ‖ ⋅‖ la norma inducida por el producto escalar ⟨ ⋅, ⋅⟩. Demostrar que para cada vector 𝑥 ∈𝐸 se cumple la igualdad ‖(𝜓+𝜙)(𝑥)‖=‖(𝜓−𝜙)(𝑥)‖.
  4. Sea ℎ =(𝜓 +𝜙) ∘(𝜓 −𝜙)−1. Se cumple que ‖ℎ(𝑥)‖ =‖𝑥‖ para todo 𝑥 ∈𝐸.
  5. Se cumple la igualdad ⟨ℎ(𝑥),ℎ(𝑦)⟩ =⟨𝑥,𝑦⟩ para cualesquiera 𝑥,𝑦 ∈𝐸.

Problema 23

Tres máquinas 𝐴, 𝐵 y 𝐶 producen una barra metálica. La longitud de las fabricadas por la máquina 𝐴 se distribuye según una distribución normal de parámetros 𝜇𝐴 =165 y 𝜎𝐴 =5. La longitud de las fabricadas por la máquina 𝐵 se distribuye según una distribución normal de parámetros 𝜇𝐵 =175 y 𝜎𝐵 =5, mientras que la longitud de las fabricadas por la máquina 𝐶 se distribuye según una distribución normal de parámetros 𝜇𝐶 =170 y 𝜎𝐶 =5. En todos los casos la longitud viene expresada en milímetros.

  1. El 50% de la producción de la fábrica la hace la máquina 𝐴, el 20% la realiza la máquina 𝐵 y el resto lo elabora la máquina 𝐶. Se eligen tres piezas al azar y se sabe que miden más de 173 mm cada una. ¿Cuál es la probabilidad de que las tres procedan de la máquina 𝐶?
  2. Si se eligen al azar, de forma independiente, 100 piezas fabricadas por la máquina 𝐵, calcular la probabilidad de que al menos 60 de ellas midan más de 173 milímetros.

Resolución

Sean 𝑋𝐴, 𝑋𝐵 y 𝑋𝐶 las longitudes en milímetros de las barras fabricadas por las máquinas A, B, y C, respectivamente. Se tiene que 𝑋𝐴 ∼𝑁(165,5), 𝑋𝐵 ∼𝑁(175,5) y 𝑋𝐶 ∼𝑁(170,5).

  1. Sean los sucesos: 𝐴=𝑠𝑒𝑟 𝑝𝑟𝑜𝑑𝑢𝑐𝑖𝑑𝑎 𝑝𝑜𝑟 𝑙𝑎 𝑚á𝑞𝑢𝑖𝑛𝑎 𝐴,𝐵=𝑠𝑒𝑟 𝑝𝑟𝑜𝑑𝑢𝑐𝑖𝑑𝑎 𝑝𝑜𝑟 𝑙𝑎 𝑚á𝑞𝑢𝑖𝑛𝑎 𝐵,𝐶=𝑠𝑒𝑟 𝑝𝑟𝑜𝑑𝑢𝑐𝑖𝑑𝑎 𝑝𝑜𝑟 𝑙𝑎 𝑚á𝑞𝑢𝑖𝑛𝑎 𝐶,𝑀=𝑚𝑒𝑑𝑖𝑟 𝑚á𝑠 𝑑𝑒 173 𝑚𝑖𝑙í𝑚𝑒𝑡𝑟𝑜𝑠. Sabemos que: 𝑃(𝐴)=0,5,𝑃(𝐵)=0,2,𝑃(𝐶)=0,3. Calculamos las probabilidades condicionadas. 𝑃(𝑀|𝐴)=𝑃(𝑋𝐴>173)=𝑃(𝑍>1,6)=1−𝑃(𝑍<1,6)=0,0548,𝑃(𝑀|𝐵)=𝑃(𝑋𝐵>173)=𝑃(𝑍>−0,4)=𝑃(𝑍<0,4)=0,6554,𝑃(𝑀|𝐶)=𝑃(𝑋𝐶>173)=𝑃(𝑍>0,6)=1−𝑃(𝑍<0,6)=0,2743. Podemos organizar los datos en un diagrama de árbol.
    𝑀
    0,0548←←←←←←←←←←←←←←→
    𝐴
    0,5←←←←←←←←←←→ 0,9452←←←←←←←←←←←←←←→
    𝑀𝑐
    𝑀
    0,6554←←←←←←←←←←←←←←→
    0,2←←←←←←←←←←→ 𝐵
    0,34446←←←←←←←←←←←←←←←→
    𝑀𝑐
    𝑀
    0,3←←←←←←←←←←→ 0,2743←←←←←←←←←←←←←←→
    𝐶
    0,7257←←←←←←←←←←←←←←→
    𝑀𝑐
    Por el teorema de la probabilidad total, la probabilidad de que una pieza mida más de 173 milímetros es: 𝑃(𝑀)=𝑃(𝑀∩𝐴)+𝑃(𝑀∩𝐵)+𝑃(𝑀∩𝐶)=𝑃(𝐴)⋅𝑃(𝑀|𝐴)+𝑃(𝐵)⋅𝑃(𝑀|𝐵)+𝑃(𝐶)⋅𝑃(𝑀|𝐶)==0,5⋅0,0548+0,2⋅0,6554+0,3⋅0,2743=0,24077. Así que la probabilidad de que una pieza proceda de C sabiendo que mide más de 173 milímetros es: 𝑃(𝐶|𝑀)=𝑃(𝐶∩𝑀)𝑃(𝑀)=𝑃(𝐶)⋅𝑃(𝑀|𝐶)𝑃(𝑀)=0,3⋅0,27430,24077≈0,3418. Por tanto, como las tres piezas son independientes, la probabilidad de que las tres procedan de 𝐶 sabiendo que miden más de 173 milímetros es: 𝑃(𝐶|𝑀)3=0,34183≈0,04.
  2. Sea 𝑝 =𝑃(𝑀|𝐵) =0,6554 y sea 𝑌 el número de piezas de 𝐵 que miden más de 173 milímetros. Entonces 𝑌 ∼Bi⁡(𝑛 =100,𝑝). Como 𝑛 =100 >30, por el teorema central del límite podemos aproximar 𝑌 a una normal con: 𝜇=𝑛𝑝=100⋅0,6554=65,54,𝜎2=𝑛𝑝(1−𝑝)=100⋅0,6554⋅0,3446≈22,5851. Por tanto, podemos aproximar: 𝑃(𝑌≥60)=𝑃(𝑌>59,5)≈𝑃(𝑍≥59,5−65,54√22,5851)=𝑃(𝑍≥−1,27)=𝑃(𝑍≤1,27)=0,898.

Problema 24

Dado el siguiente sistema de ecuaciones: ⎧{ {⎨{ {⎩𝑎𝑥+(2𝑎+1)𝑦−𝑎𝑧=1,𝑎𝑥+𝑦−𝑎𝑧=−2𝑏,𝑎𝑦+(1−𝑎)𝑧=𝑏.

  1. Discutir y resolver el sistema.
  2. Situar el problema dentro de un curso de la Educación Secundaria Obligatoria o Bachillerato, indicando los conocimientos previos que debe poseer el alumnado, las posibles relaciones con otras ramas de la matemática y/o con otras materias, las diversas alternativas para su resolución, los recursos y medios que se podrían utilizar, los posibles instrumentos de evaluación y otros aspectos de carácter didáctico que se consideren significativos.

Problema 25

La duración en minutos de una llamada telefónica de larga distancia viene dada por una variable aleatoria 𝑋 cuya función de distribución es: 𝐹𝑋(𝑥)={0,si 𝑥≤0,1−23𝑒−2𝑥/3−13𝑒−𝑥/3,si 𝑥>0.

  1. Encuentre la función de densidad de 𝑋.
  2. Calcule la esperanza matemática o duración media de las llamadas.
  3. Calcule la probabilidad de que la duración de una llamada telefónica esté comprendida entre 3 y 6 minutos.
  4. Calcule la probabilidad de que una llamada cuya duración excede los tres minutos no dure más de 6 minutos.

Resolución
  1. La función de densidad viene dada por la derivada de la función de distribución. 𝑓𝑋(𝑥)=𝐹′𝑋(𝑥)={0,si 𝑥≤0,49𝑒−2𝑥/3+19𝑒−𝑥/3,si 𝑥>0.
  2. Calculamos la esperanza de 𝑋. 𝐸(𝑋)=∫ℝ𝑥𝑓(𝑥)𝑑𝑥=∫+∞0(49𝑥𝑒−2𝑥/3+19𝑥𝑒−𝑥/3)𝑑𝑥=23∫+∞023𝑥𝑒−2𝑥/3𝑑𝑥+13∫+∞013𝑥𝑒−𝑥/3𝑑𝑥. Integramos por partes. (1)𝑢=𝑥⇒𝑢′=1,(2)𝑢=𝑥⇒𝑢′=1,𝑣′=23𝑒−2𝑥/3⇒𝑣=−𝑒−2𝑥/3,𝑣′=13𝑒−𝑥/3⇒𝑣=−𝑒−𝑥/3. Por tanto, 𝐸(𝑋)=[−23𝑥𝑒−2𝑥/3]+∞0+∫+∞023𝑒−2𝑥/3𝑑𝑥+[−13𝑥𝑒−𝑥/3]+∞0+∫+∞013𝑒−𝑥/3𝑑𝑥==[−𝑥𝑒−2𝑥/3]+∞0+[−𝑥𝑒−2𝑥/3]+∞0=2.
  3. La probabilidad de que la duración de una llamada esté comprendida entre 3 y 6 minutos es: 𝑃(3<𝑋<6)=𝐹(6)−𝐹(3)=1−23𝑒−4−13𝑒−2−(1−23𝑒−2−13𝑒−1)=13𝑒+13𝑒2−23𝑒4≈0,1556.
  4. La probabilidad de que una llamada exceda los tres minutos es: 𝑃(𝑋>3)=1−𝑃(𝑋<3)=1−𝐹(3)=1−(1−23𝑒2−13𝑒)=23𝑒2+13𝑒≈0,2129. Por tanto, la probabilidad de que una llamada no dure más de seis minutos dado que ha excedido los tres minutos es: 𝑃(𝑋<6|𝑋>3)=𝑃(3<𝑋<6)𝑃(𝑋>3)=0,15560,2129≈0,7307.

Problema 26

Un juego consiste en extraer dos bolas, con reemplazamiento, de una bolsa que contiene una bola blanca y una negra. Si las dos bolas son blancas, se gana el juego. Si no, se introduce en la bolsa otra bola negra y se efectúan dos nuevas extracciones, y este proceso se repite indefinidamente. ¿Cuál es la probabilidad de ganar el juego?

Resolución

Sean los sucesos: 𝐺𝑛=𝑔𝑎𝑛𝑎𝑟 𝑒𝑙 𝑗𝑢𝑒𝑔𝑜 𝑒𝑛 𝑒𝑙 𝑖𝑛𝑡𝑒𝑛𝑡𝑜 𝑛,𝑛=1,2,…,𝐺=𝑔𝑎𝑛𝑎𝑟 𝑒𝑙 𝑗𝑢𝑒𝑔𝑜. Los sucesos 𝐺𝑛 son incompatibles dos a dos y se tiene que: 𝑃(𝐺)=∞⋃𝑛=1𝐺𝑛.

Observamos que: 𝑃(𝐺1)=(12)2=14,𝑃(𝐺2)=[1−(12)2]⋅(13)2=112,𝑃(𝐺3)=[1−(12)2]⋅[1−(13)2]⋅(14)2=124. Dado 𝑛 ∈ℕ, 𝑃(𝐺𝑛)=𝑛−1∏𝑖=1(1−1(𝑖+1)2)⋅1(𝑛+1)2=1(𝑛+1)2𝑛−1∏𝑖=1(𝑖+1)2−1(𝑖+1)2=1(𝑛+1)2𝑛−1∏𝑖=1𝑖(𝑖+2)(𝑖+1)2. Observamos que: 𝑛−1∏𝑖=1𝑖(𝑖+2)(𝑖+1)2=1⋅322⋅2⋅432⋅3⋅542⋅4⋅652⋅…⋅(𝑛−1)⋅(𝑛+1)𝑛2=12⋅𝑛+1𝑛=𝑛+12𝑛. Así que: 𝑃(𝐺𝑛)=1(𝑛+1)2𝑛−1∏𝑖=1𝑖(𝑖+2)(𝑖+1)2=1(𝑛+1)2⋅𝑛+12𝑛=12𝑛(𝑛+1).

Por tanto, 𝑃(𝐺)=∞∑𝑛=1𝑃(𝐺𝑛)=12∞∑𝑛=11𝑛(𝑛+1). Descomponemos en suma de fracciones simples. 1𝑛(𝑛+1)=𝐴𝑛+𝐵𝑛+1=𝐴(𝑛+1)+𝐵𝑛𝑛(𝑛+1).

  • Si 𝑛 =0, entonces 𝐴 =1.
  • Si 𝑛 = −1, entonces −𝐵 =1 ⇔𝐵 =1.

De esta forma, 1𝑛(𝑛+1)=1𝑛−1𝑛+1. Luego: ∞∑𝑛=11𝑛(𝑛+1)=∞∑𝑛=1(1𝑛−1𝑛+1)=11−12+12−13+13−14+…=1. Por tanto, la probabilidad de ganar el juego es: 𝑃(𝐺)=12∞∑𝑛=11𝑛(𝑛+1)=12.

Problema 27

En un determinado país se padece la enfermedad endémica 𝑋, y unos laboratorios han desarrollado un test para detectar la enfermedad. Este test da positivo al 99% de las personas que la padecen. Este valor se denomina sensibilidad del test. Además, el test arroja un resultado negativo en el 95% de las personas que no la padecen. Este valor recibe el nombre de especificidad del test.

  1. Resolver las siguientes cuestiones:
    1. Si la proporción de personas en el país que padecen la enfermedad 𝑋 es 𝑝 =0.02, calcular el valor predictivo positivo del test, es decir, la probabilidad de que una persona esté enferma si el test ha dado positivo. Calcular también el valor predictivo negativo del test, es decir, la probabilidad de que una persona cuyo test ha dado negativo no padezca la enfermedad.
    2. Si ahora la proporción de enfermos es 𝑝, donde 0 ≤𝑝 ≤1, escribir el valor predictivo positivo como una función de 𝑝, si tanto la sensibilidad como la especificidad del test son los del enunciado. Determinar si es una función creciente y calcular su valor máximo.
    3. En las condiciones del apartado anterior determinar cuál debe ser la proporción mínima de enfermos con la enfermedad 𝑋 en este país para que el valor predictivo positivo sea, al menos, el 75%.
  2. Situar el problema dentro de un curso de la Educación Secundaria Obligatoria o Bachillerato, indicando los conocimientos previos que debe poseer el alumnado, las posibles relaciones con otras ramas de la matemática y/o con otras materias, las diversas alternativas para su resolución, los recursos y medios que se podrían utilizar, los posibles instrumentos de evaluación y otros aspectos de carácter didáctico que se consideren significativos.

Problema 28

Se desliza un cuadrado cuyo lado mide 10 cm situado en el primer cuadrante del plano 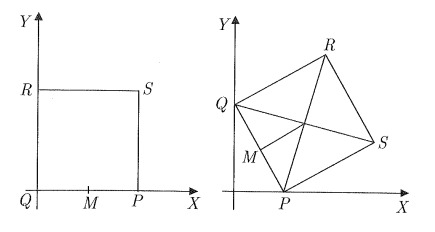𝑂𝑋𝑌 de manera que los vértices de uno de sus lados estén siempre en contacto con los ejes coordenados: uno con el eje 𝑂𝑋 y otro con el eje 𝑂𝑌. Figura Con las notaciones de la figura, en las que se muestran la posición inicial del cuadrado y una de las posiciones intermedias, determinar el lugar geométrico descrito por los siguientes puntos:

  1. El punto medio 𝑀 del lado cuyos vértices están situados uno en cada eje.
  2. El centro 𝐶′ del cuadrado.
  3. El vértice 𝑃.
  4. El vértice 𝑄.