Problema 1
Se corta por un plano paralelo a una generatriz un cono equilátero de lado 10. Se pide el área del segmento parabólico así obtenido cuando esta área es máxima.
Se corta por un plano paralelo a una generatriz un cono equilátero de lado 10. Se pide el área del segmento parabólico así obtenido cuando esta área es máxima.
Sea la matriz
En un triángulo 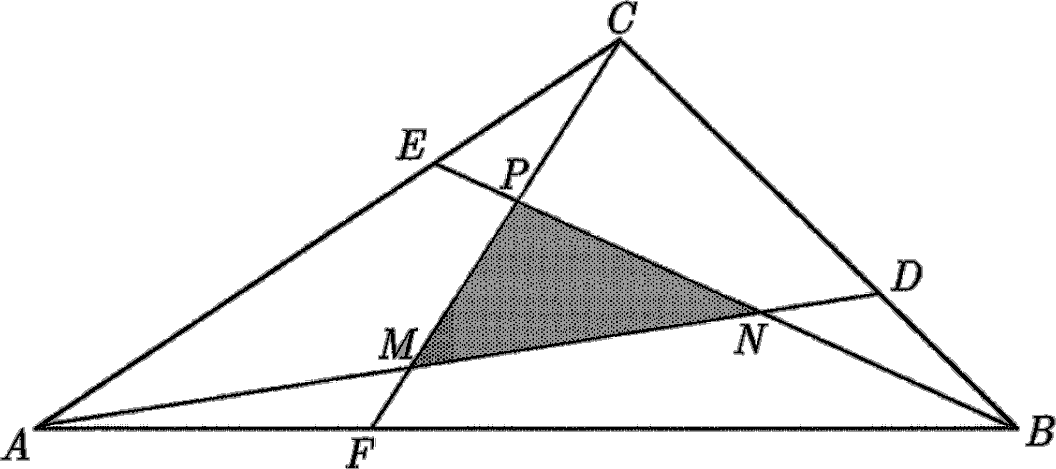
Se tienen