Icono Matemáticas de oposiciones

GitHub

📋 Examen de 2018 de Andalucía

Problema 1

Dada la matriz 𝐴 ∈ℝ4×3, el vector 𝑏 ∈ℝ4, 𝛼 ∈ℝ y el subespacio 𝐹 de ℝ4 𝐴=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝−12001−1−11101−1⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠,𝑏=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝01𝛼−2𝛼2⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠y𝐹≡{𝑥1+𝑥2−𝑥4=0,𝑥1+𝑥3+𝑥4=0.

  1. Discutir y resolver cuando sea compatible el sistema 𝐴𝑋 =𝑏, con 𝑋 ∈ℝ3.
  2. Sea 𝐸 el espacio columna de 𝐴, calcular sus ecuaciones implícitas.
  3. Encontrar una base del subespacio 𝐸 ∩𝐹.
  4. Calcular la matriz 𝐵 de la transformación lineal 𝑇 :ℝ3 →ℝ4 que verifica: 𝑇(𝑒1)=𝐴(𝑒2+𝑒3),𝑇(𝑒2)=𝐴𝑒3,𝑇(𝑒3)=𝐴𝑒2, donde {𝑒1,𝑒2,𝑒3} es la base canónica de ℝ3.

Resolución
  1. Para hallar el rango de la matriz de coeficientes 𝐴 y la matriz ampliada 𝐴∗, realizamos transformaciones elementales. 𝐴∗=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝−120001−11−111𝛼−201−1𝛼2⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠𝐹3−𝐹1←←←←←←←←←←→𝐹4−𝐹2⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝−120001−110−11𝛼−2000𝛼2−1⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠𝐹3+𝐹2←←←←←←←←←←→⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝−120001−11000𝛼−1000𝛼2−1⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠. Observamos que rang⁡(𝐴) =2 para todo 𝛼 ∈ℝ. Estudiamos el rango de la matriz ampliada en función de 𝛼.
    • Si 𝛼 ≠ ±1, rang⁡(𝐴∗) =4. Por el teorema de Rouché-Frobenius, el sistema es incompatible.
    • Si 𝛼 = −1, rang⁡(𝐴∗) =3. Por el teorema de Rouché-Frobenius, el sistema es incompatible.
    • Si 𝛼 =1, rang⁡(𝐴∗) =2. Por el teorema de Rouché-Frobenius, el sistema es compatible indeterminado.
    Para 𝛼 =1, el sistema se puede reducir a: {−𝑥1+2𝑥2=0,𝑥2−𝑥3=0. Por tanto, si tomamos 𝑦 =𝜆, las soluciones del sistema son de la forma: ⎧{ {⎨{ {⎩𝑥1=2𝜆,𝑥2=𝜆,𝑥3=𝜆−1,𝜆∈ℝ.
  2. El espacio 𝐸 está generado por los vectores columna de 𝐴. Como rang⁡(𝐴) =2, se tiene que: 𝐸=⟨⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝−10−10⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠,⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝2111⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠,⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝0−11−1⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠⟩=⟨⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝−10−10⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠,⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝2111⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠⟩. Se puede expresar como: 𝐸:⎧{ { {⎨{ { {⎩𝑥1=−𝜆+2𝜇,𝑥2=𝜇,𝑥3=−𝜆+𝜇,𝑥4=𝜇⇔{𝑥1−𝑥3=𝑥2,𝑥2=𝑥4.⇔{𝑥1−𝑥2−𝑥3=0,𝑥2−𝑥4=0.
  3. Hallamos el subespacio 𝐸 ∩𝐹. 𝐸∩𝐹:⎧{ { {⎨{ { {⎩𝑥1−𝑥2−𝑥3=0,𝑥2−𝑥4=0,𝑥1+𝑥2−𝑥4=0,𝑥1+𝑥3+𝑥4=0⇔⎧{ {⎨{ {⎩𝑥2=𝑥4,𝑥1=0,𝑥3=−𝑥4⇔⎧{ { {⎨{ { {⎩𝑥1=0,𝑥2=𝜆,𝑥3=−𝜆,𝑥4=𝜆⇔𝐸∩𝐹=⟨⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝01−11⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠⟩.
  4. La transformación lineal 𝑇 verifica: 𝑇(𝑒1)=𝐴(𝑒2+𝑒3)=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝−12001−1−11101−1⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝011⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝2020⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠,𝑇(𝑒2)=𝐴𝑒3=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝−12001−1−11101−1⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝001⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝0−11−1⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠,𝑇(𝑒3)=𝐴𝑒2=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝−12001−1−11101−1⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝010⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝2111⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠. Por tanto, 𝐵=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝2020−112110−11⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠.

Problema 2

Dados los puntos del plano 𝐴(1,2) y 𝐵(3,3), se pide:

  1. Calcular la ecuación de la parábola que tiene el vértice en el punto 𝐴 y el foco en punto 𝐵.
  2. Determinar como número complejo en forma binomica los vértices de un triángulo equilátero con centro en 𝐴, sabiendo que 𝐵 es uno de sus vértices.

Resolución
  1. En primer lugar, hallamos la directriz de la parábola. El vértice 𝐴 equidista del foco y la directriz, así que podemos hallar un punto 𝐵′ de la directriz como el simétrico de 𝐵 respecto de 𝐴. Sea 𝐵′(𝑥,𝑦), se tiene que: {3+𝑥2=1⇔𝑥=−1,3+𝑦2=2⇔𝑦=1. Luego 𝐵′( −1,1) es un punto de la directriz. Por otro lado, el eje de simetría de la parábola pasa por los puntos 𝐴 y 𝐵, así que su pendiente es 𝑚𝑒 =12. Como la directriz es perpendicular al eje de simetría, la pendiente de la directriz es 𝑚𝑑 = −2. Por tanto, la ecuación de la directriz es: 𝑟≡𝑦−1=−2(𝑥+1)⇔2𝑥+𝑦+1=0. La parábola es el lugar geométrico de los puntos del plano que equisitan del foco y la directriz. Sea 𝑃(𝑥,𝑦) un punto de la parábola, entonces se tiene que: dist⁡(𝑃,𝐵)=dist⁡(𝑃,𝑟)⇔√(3−𝑥)2+(3−𝑦)2=|2𝑥+𝑦+1|√5⇔⇔9+𝑥2−6𝑥+9+𝑦2−6𝑦=(2𝑥+𝑦+1)25⇔⇔5𝑥2+5𝑦2−30𝑥−30𝑦+90=4𝑥2+4𝑥𝑦+4𝑥+𝑦2+2𝑦+1⇔⇔𝑥2+4𝑦2−4𝑥𝑦−34𝑥−32𝑦+89=0.
  2. Sean 𝑧𝐴 =1 +2𝑖 y 𝑧𝐵 =3 +3𝑖. En primer lugar, trasladamos el centro del triángulo al origen de coordenadas. De esta forma, el vértice 𝑧𝐵 se transforma en: 𝑧1=𝑧𝐵−𝑧𝐴=2+𝑖=√5𝑒𝛼𝑖,con 𝛼=arctg⁡(12). Las razones trigonométricas del ángulo 𝛼 son: sen⁡(𝛼)=1√5,cos⁡(𝛼)=2√5. Los otros dos vértices del triángulo equilátero trasladado son de la forma: 𝑧2=√5𝑒(𝛼+2𝜋3)𝑖=√5cos⁡(𝛼+2𝜋3)+√5sen⁡(𝛼+2𝜋3)𝑖,𝑧3=√5𝑒(𝛼+4𝜋3)𝑖=√5cos⁡(𝛼+4𝜋3)+√5sen⁡(𝛼+4𝜋3)𝑖. De esta forma, calculamos: cos⁡(𝛼+2𝜋3)=cos⁡(𝛼)cos⁡(2𝜋3)−sen⁡(𝛼)sen⁡(2𝜋3)=2√5⋅(−12)−1√5⋅√32=−1√5−√32√5,sen⁡(𝛼+2𝜋3)=sen⁡(𝛼)cos⁡(2𝜋3)+cos⁡(𝛼)sen⁡(2𝜋3)=1√5⋅(−12)+2√5⋅√32=−12√5+√3√5,cos⁡(𝛼+4𝜋3)=cos⁡(𝛼)cos⁡(4𝜋3)−sen⁡(𝛼)sen⁡(4𝜋3)=2√5⋅(−12)−1√5⋅(−√32)=−1√5+√32√5,sen⁡(𝛼+4𝜋3)=sen⁡(𝛼)cos⁡(4𝜋3)+cos⁡(𝛼)sen⁡(4𝜋3)=1√5⋅(−12)+2√5⋅(−√32)=−12√5−√3√5. Así que: 𝑧2=√5cos⁡(𝛼+2𝜋3)+√5sen⁡(𝛼+2𝜋3)𝑖=−1−√32+(−12+√3)𝑖,𝑧3=√5cos⁡(𝛼+4𝜋3)+√5sen⁡(𝛼+4𝜋3)𝑖=−1+√32+(−12−√3)𝑖. Por tanto, los vértices del triángulo equilátero son: 𝑧𝐵=3+3𝑖,𝑧𝐶=𝑧2+𝑧𝐴=−√32+(32+√3)𝑖=−√32+3+2√32𝑖,𝑧𝐷=𝑧3+𝑧𝐴=√32+(32−√3)𝑖=√32+3−2√32𝑖.

Problema 3

Consideramos la curva 𝐶 de ecuacion: 𝑥2 +𝑦2 =4.

  1. De todos los triángulos inscritos en la curva 𝐶, con vértice en el punto 𝐴(0,2) y base paralela al eje 𝑂𝑋, calcular el que tiene máxima superficie.
  2. Calcular la ecuacion de la envolvente de la familia de las circunferencias que tienen el centro en la curva 𝐶 y que sus radios son la mitad del radio 𝐶.

Resolución
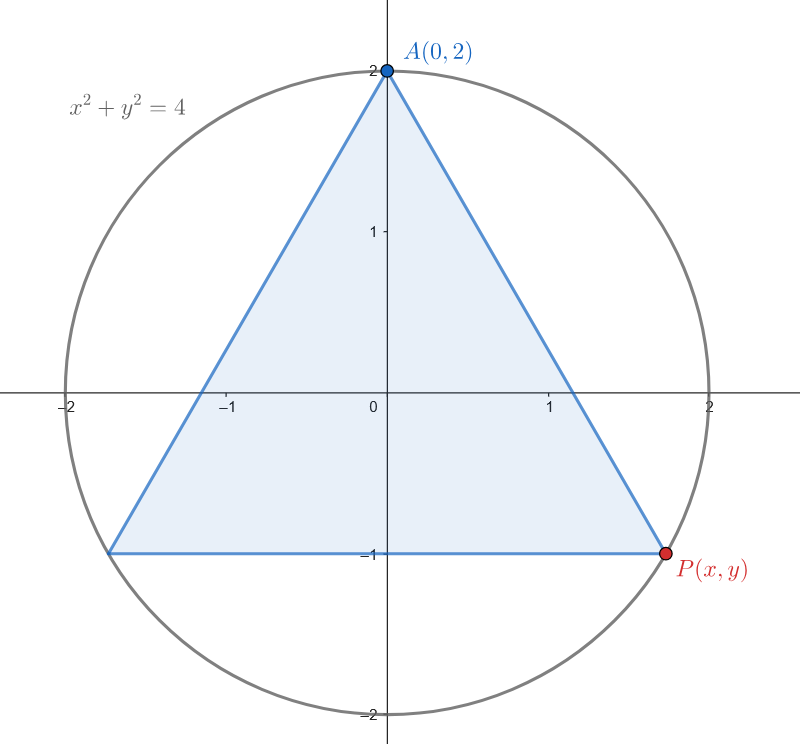  1. Sea 𝑃(𝑥,𝑦) el vértice del triángulo en el semiplano derecho, es decir, con 𝑥 >0. Figura Observamos que la base del triángulo es 2𝑥 y su altura es 2 −𝑦. Así que el área del triángulo viene dada por: 𝑆=2𝑥⋅(2−𝑦)2=𝑥(2−𝑦). Como está inscrito en la circunferencia de ecuación 𝑥2 +𝑦2 =4, se verifica que 𝑥 =√4−𝑦2. Luego la función a maximizar es: 𝑆(𝑦)=(2−𝑦)√4−𝑦2. En primer lugar, hallamos la derivada de la función 𝑆. 𝑆′(𝑦)=−√4−𝑦2+(2−𝑦)⋅−2𝑦2√4−𝑦2=−√4−𝑦2−𝑦(2−𝑦)√4−𝑦2. Hallamos los puntos críticos de 𝑆 igualando la derivada a cero. 𝑆′(𝑦)=0⇔−√4−𝑦2−𝑦(2−𝑦)√4−𝑦2=0⇔−𝑦(2−𝑦)√4−𝑦2⇔√4−𝑦2=−2𝑦+𝑦2=4−𝑦2⇔⇔2𝑦2−2𝑦−4=0⇔𝑦2−𝑦−2=0⇔{𝑦=−1,𝑦=2. Como 𝑃 es un vértice distinto de 𝐴, la solución 𝑦 =2 no es válida. Comprobamos que se alcanza el máximo en 𝑦 = −1.
    • Si −2 <𝑦 < −1, 𝑆′(𝑦) >0. Así que 𝑆 es creciente.
    • Si −1 <𝑦 <2, 𝑆′(𝑦) <0. Así que 𝑆 es decreciente.
    Luego 𝑆 alcanza el mínimo en 𝑦 = −1, así que 𝑥 =√3. Por tanto, el triángulo de área máxima es el de vértices 𝐴(0,2), 𝐵(√3, −1) y 𝐶( −√3, −1).
  2. En primer lugar, expresamos la curva 𝐶 ≡𝑥2 +𝑦2 =4 en ecuaciones paramétricas: {𝑥=2cos⁡(𝑡),𝑦=2sen⁡(𝑡),𝑡∈[0,2𝜋]. La familia de curvas con centro en 𝐶 y radio 1 viene dada por la ecuación: (𝑥−2cos⁡(𝑡))2+(𝑦−2sen⁡(𝑡))2=1⇔(𝑥−2cos⁡(𝑡))2+(𝑦−2sen⁡(𝑡))2−1=0. Sea 𝐹(𝑥,𝑦,𝑡) =(𝑥 −2cos⁡(𝑡))2 +(𝑦 −2sen⁡(𝑡))2 −1. La ecuación de la envolvente viene dada por: ⎧{ {⎨{ {⎩𝐹(𝑥,𝑦,𝑡)=0,𝜕𝐹(𝑥,𝑦,𝑡)𝜕𝑡=0⇔{(𝑥−2cos⁡(𝑡))2+(𝑦−2sen⁡(𝑡))2−1=0,2(𝑥−2cos⁡(𝑡))⋅2sen⁡(𝑡)+2(𝑦−2sen⁡(𝑡))⋅(−2cos⁡(𝑡))=0⇔{𝑥2−4𝑥cos⁡(𝑡)+4cos2⁡(𝑡)+𝑦2−4𝑦sen⁡(𝑡)+4sen2⁡(𝑡)−1=0,𝑥sen⁡(𝑡)−2sen⁡(𝑡)cos⁡(𝑡)−𝑦cos⁡(𝑡)+2sen⁡(𝑡)cos⁡(𝑡)=0⇔{4𝑥cos⁡(𝑡)+4𝑦sen⁡(𝑡)=𝑥2+𝑦2+3,𝑥sen⁡(𝑡)−𝑦cos⁡(𝑡)=0. Despejando en la segunda ecuación, 𝑥sen⁡(𝑡)−𝑦cos⁡(𝑡)=0⇔𝑥sen⁡(𝑡)=𝑦cos⁡(𝑡)⇔tg⁡(𝑡)=𝑦𝑥. Luego se tiene que: sen⁡(𝑡)=𝑦√𝑥2+𝑦2ycos⁡(𝑡)=𝑥√𝑥2+𝑦2. Sustituyendo en la primera ecuación, obtenemos que: 4𝑥2√𝑥2+𝑦2+4𝑦2√𝑥2+𝑦2=𝑥2+𝑦2+3⇔4√𝑥2+𝑦2=𝑥2+𝑦2+3. Realizamos el cambio de variable 𝑢 =√𝑥2+𝑦2. Entonces: 4𝑢=𝑢2+3⇔𝑢2−4𝑢+3=0⇔{𝑢=1⇔√𝑥2+𝑦2=1⇔𝑥2+𝑦2=1,𝑢=3⇔√𝑥2+𝑦2=3⇔𝑥2+𝑦2=9.

Problema 4

Consideramos la función 𝑓(𝑥) =cos⁡(𝑥).

  1. Calcular la serie de Taylor de la función 𝑓.
  2. Demostrar que: ∫10cos⁡(𝑥)2√𝑥𝑑𝑥=∞∑𝑛=0(−1)𝑛(4𝑛+1)(2𝑛)!.
  3. Calcula el valor de ∫10cos⁡(𝑥)2√𝑥𝑑𝑥 con un error menor que 10−3.

Resolución
  1. La función 𝑓(𝑥) =cos⁡(𝑥) es de clase C∞, con derivadas sucesivas: 𝑓′(𝑥)=−sen⁡(𝑥),𝑓″(𝑥)=−cos⁡(𝑥),𝑓‴(𝑥)sen⁡(𝑥),𝑓(𝐼𝑉)(𝑥)=cos⁡(𝑥)=𝑓(𝑥). Como |𝑓(𝑛)(𝑥)| ≤1 para todo 𝑛 ∈ℕ y todo 𝑥 ∈ℝ, 𝑓 es desarrollable en serie de potencias en ℝ. La serie de Taylor centrada en 𝑎 de la función 𝑓 es: 𝑓(𝑥)=∞∑𝑛=0𝑓(𝑛)(𝑎)𝑛!(𝑥−𝑎)𝑛=∞∑𝑛=0(−1)𝑛cos⁡(𝑎)(2𝑛)!(𝑥−𝑎)2𝑛+∞∑𝑛=0(−1)𝑛+1sen⁡(𝑎)(2𝑛+1)!(𝑥−𝑎)2𝑛+1,𝑥∈ℝ. En particular, la serie de Taylor centrada en 0 de la función es: 𝑓(𝑥)=∞∑𝑛=0(−1)𝑛𝑥2𝑛(2𝑛)!,𝑥∈ℝ.
  2. Usamos la serie de Taylor centrada en 0 de la función. ∫10cos⁡(𝑥)2√𝑥𝑑𝑥=∫10(12√𝑥∞∑𝑛=0(−1)𝑛𝑥2𝑛(2𝑛)!)𝑑𝑥=∫10(∞∑𝑛=0(−1)𝑛𝑥2𝑛(2𝑛)!⋅12√𝑥)𝑑𝑥==∞∑𝑛=0(∫10(−1)𝑛𝑥2𝑛(2𝑛)!⋅12√𝑥𝑑𝑥)=∞∑𝑛=0((−1)𝑛(2𝑛)!∫10𝑥2𝑛2√𝑥𝑑𝑥)==∞∑𝑛=0((−1)𝑛(2𝑛)!⋅12∫10𝑥2𝑛−12𝑑𝑥)=∞∑𝑛=0(−1)𝑛(2𝑛)!⋅12[12𝑛+12𝑥2𝑛+12]10==∞∑𝑛=0(−1)𝑛(2𝑛)!⋅12(2𝑛+12)=∞∑𝑛=0(−1)𝑛(4𝑛+1)(2𝑛)!.
  3. Usamos la igualdad del apartado anterior. Sean: 𝑎𝑛=(−1)𝑛(4𝑛+1)(2𝑛)!y𝑆𝑛=𝑛∑𝑘=0𝑎𝑘. Como 𝑎𝑛 es monótona decreciente y tiende a cero, el error al aproximar la integral por 𝑆𝑛 es menor que 𝑎𝑛+1. Hallamos los primeros términos de la sucesión. 𝑎0=1,𝑎1=−110,𝑎2=1216,𝑎4=−19.360<10−3. Por tanto, podemos aproximar: ∫10cos⁡(𝑥)2√𝑥𝑑𝑥≈𝑆2=1−110+1216≈0,9046, con un error menor que 10−3.

Problema 5

Consideramos las funciones 𝑓(𝑥) =𝑥𝑒−𝑥 y 𝑔(𝑥) =2 −𝑥∫𝑥0𝑒−𝑡2𝑑𝑡.

  1. Estudiar y representar gráficamente la función 𝑓.
  2. Calcular: lím𝑥→0⁡𝑓(𝑥)−𝑔(𝑥)+2−𝑥𝑥ln⁡(1−𝑥).

Resolución
  1. El dominio de la función es Dom⁡(𝑓) =ℝ. Observamos que (0,0) es el único punto de corte con los ejes coordenados y no presenta simetría. Se trata además de una función continua y derivable en todo su dominio.
    • Estudiamos la existencia de asíntotas horizontales. lím𝑥→−∞⁡𝑓(𝑥)=lím𝑥→−∞⁡𝑥𝑒−𝑥=−∞,lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡𝑥𝑒−𝑥=0. Luego la recta 𝑦 =0 es una asíntota horizontal por la derecha. Como no es una función racional, no tiene asíntota oblicua por la izquierda.
    • Para estudiar su monotonía, hallamos en primer lugar la derivada de la función. 𝑓′(𝑥)=𝑒−𝑥−𝑥𝑒−𝑥=(−𝑥+1)𝑒−𝑥. Hallamos los puntos críticos igualando la derivada a cero. 𝑓′(𝑥)=0⇔(−𝑥+1)𝑒−𝑥=0⇔−𝑥+1=0⇔𝑥=1. Estudiamos el signo de la derivada.
      • Si 𝑥 <1, 𝑓′(𝑥) >0. Así que 𝑓 es creciente.
      • Si 𝑥 >1, 𝑓′(𝑥) <0. Así que 𝑓 es decreciente.
      Luego 𝑓 es creciente en ( −∞,1) y decreciente en (1, +∞), con el punto (1,1𝑒) como máximo absoluto.
    • Para estudiar su curvatura, hallamos su segunda derivada. 𝑓″(𝑥)=−𝑒−𝑥−(−𝑥+1)𝑒−𝑥=(𝑥−2)𝑒−𝑥. Hallamos los candidatos a puntos de inflexión igualando la segunda derivada a cero. 𝑓″(𝑥)=0⇔(𝑥−2)𝑒−𝑥=0⇔𝑥−2=0⇔𝑥=2. Estudiamos el signo de la segunda derivada.
      • Si 𝑥 <2, 𝑓″(𝑥) <0. Así que 𝑓 es cóncava.
      • Si 𝑥 >2, 𝑓″(𝑥) >0. Así que 𝑓 es convexa.
      Luego 𝑓 es convexa en (2, +∞) y cóncava en ( −∞,2), con el punto de inflexión (2,2𝑒2).
    Representamos la gráfica de la función con toda esta información. Figura
  2. Calculamos el límite. lím𝑥→0⁡𝑓(𝑥)−𝑔(𝑥)+2−𝑥𝑥ln⁡(1−𝑥)=lím𝑥→0⁡𝑥𝑒−𝑥−2+𝑥∫𝑥0𝑒−𝑡2𝑑𝑡+2−𝑥𝑥ln⁡(1−𝑥)=lím𝑥→0⁡𝑥𝑒−𝑥+𝑥∫𝑥0𝑒−𝑡2𝑑𝑡−𝑥𝑥ln⁡(1−𝑥)==lím𝑥→0⁡𝑒−𝑥+∫𝑥0𝑒−𝑡2𝑑𝑡−1ln⁡(1−𝑥)L’H=lím𝑥→0⁡−𝑒−𝑥+𝑒−𝑥2−11−𝑥=0. Se ha usado que la función ℎ(𝑥) =∫𝑥0𝑒−𝑡2𝑑𝑡 es derivable por el teorema fundamental del cálculo, con ℎ′(𝑥) =𝑒−𝑥2.

Problema 6

Consideremos el conjunto 𝐶 ={1,2,3,4,5}.

  1. Calcular la probabilidad de que sean reales las raíces de la ecuación 𝑥2 +𝑏𝑥 +𝑐 =0, cuando los coeficientes 𝑏 y 𝑐 se eligen al azar entre los números del conjunto 𝐶.
  2. Supongamos un dado de cinco caras numeradas con los números de 𝐶. ¿Cuál es el número mínimo de veces que habría que lanzarlo para que la probabilidad de que salga al menos una vez el número 1 sea mayor que 0,9?

Resolución
  1. Sabemos que: 𝑥2+𝑏𝑥+𝑐=0⇔𝑥=−𝑏±√𝑏2−4𝑐2. Las soluciones de esta ecuación son reales si y solo si 𝑏2 −4𝑐 ≥0, con 𝑏,𝑐 ∈𝐶. Podemos hacer una tabla para determinar el signo de 𝑏2 −4𝑐 en todos los posibles casos.
    𝑏 \ 𝑐 1 2 3 4 5
    1 − − − − −
    2 0 − − − −
    3 + + − − −
    4 + + + 0 −
    5 + + + + +
    Por tanto, la probabilidad de que las soluciones sean reales es 1225.
  2. Sea 𝑋 el número de veces que sale el número 1 al lanzar 𝑛 veces un dado de cinco caras. Observamos que 𝑋 ∼Bi⁡(𝑛,15), así que: 𝑃(𝑋=𝑘)=(𝑛𝑘)⋅(15)𝑘⋅(45)𝑛−𝑘,𝑘=0,1,…,𝑛. Se tiene que verificar que: 𝑃(𝑋≥1)>0,9⇔1−𝑃(𝑋=0)>0,9⇔𝑃(𝑋=0)<0,1⇔(45)𝑛<0,1⇔⇔𝑛log⁡(45)<−1⇔𝑛>−1log⁡(45)≈10,3189. Por tanto, hay que lanzar el dado un mínimo de 11 veces.