Icono Matemáticas de oposiciones

GitHub

📋 Examen de 2002 de Andalucía

Problema 1

Se dan las rectas: 𝑟1≡𝑥+𝑦−2=0,𝑟2≡𝑥+2𝑦−3=0,𝑟3≡3𝑥+𝑦−4=0. Hallar los vértices 𝐴, 𝐵 y 𝐶 de un triángulo sabiendo que el radio de la circunferencia es 2 y que 𝑟1 es la mediatriz de 𝐴𝐵, 𝑟2 es la de 𝐵𝐶 y 𝑟3 es la de 𝐶𝐴. ¿Cuántas soluciones hay? Hallarlas todas.

Problema 2

El triángulo equilátero ABP (ver figura adjunta) de lado unidad está dentro del cuadrado 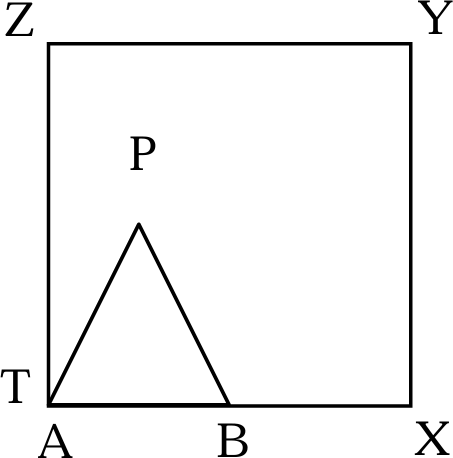𝑇𝑋𝑌𝑍 de lado 2, en una posición que llamaremos "posición inicial". El triángulo gira en sentido horario con centro en 𝐵, luego con centro en 𝑃 y así sucesivamente a lo largo de los lados del cuadrado, hasta que retorna a la "posición inicial". Figura

  1. ¿Cuál es la longitud de camino recorrido por el vértice 𝑃?
  2. ¿Y si el lado del cuadrado mide cinco unidades?
  3. Generalícese el resultado para cuando el lado del cuadrado sea igual a 3𝑛 +2 veces el lado del triángulo.

Problema 3

El problema de los repartos: Pascal (1623 - 1662) – Fermat (1601 - 1665). Dos jugadores A y B apuestan en un cierto juego equitativo 32 euros cada uno. El juego se desarrolla por partidas y gana la apuesta el primero que consiga cinco partidas. Cuando el primero ha ganado tres partidas y el segundo dos, el juego se interrumpe. ¿Cómo hay que repartir las cantidades apostadas para ser justos?

Problema 4

Representar gráficamente una función de la que se tienen los siguientes datos:

  • Sea 𝑓 una función definida, continua y derivable en ℝ ∖{ −1}.
  • La ecuación 𝑓(𝑥) =0 tiene exactamente una solución negativa, que además es única.
  • La ecuación 𝑓′(𝑥) =0 también tiene una única solución (simple) positiva.
  • Se verifica que 𝑓(0) =4 y 𝑓(1) =34.
  • La recta 𝑦 =𝑥 +1 es una asíntota oblicua.
  • lím𝑥→−1±⁡𝑓(𝑥) = +∞.
  1. Hacer la representación gráfica de la función sabiendo que es una función racional.
  2. Obtener la expresión analítica de una función.

Resolución
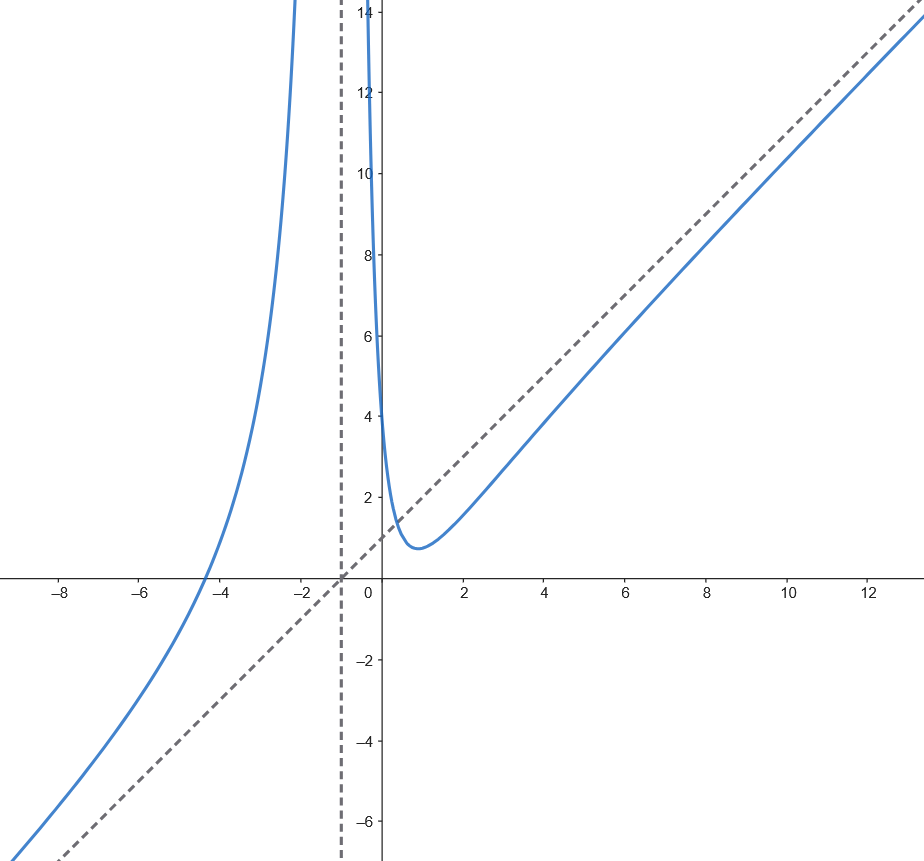
  1. Representamos gráficamente la función. Figura
  2. Sea 𝑓 :ℝ ∖{ −1} →ℝ dada por: 𝑓(𝑥)=𝑃(𝑥)𝑄(𝑥), donde 𝑃 y 𝑄 son polinomios con coeficientes reales.
    • Como Dom⁡(𝑓) =ℝ ∖{ −1} y lím𝑥→−1±⁡𝑓(𝑥) = +∞, entonces 𝑄 tiene como única raíz -1 con multiplicidad par.
    • Como la función tiene una asíntota oblicua, entonces 𝑃 debe tener un grado más que 𝑄.
    Supongamos que el grado de 𝑃 es 3 y el grado de 𝑄 es 2. Entonces la función es de la forma: 𝑓(𝑥)=𝑎𝑥3+𝑏𝑥2+𝑐𝑥+𝑑𝑒(𝑥+1)2. Como la pendiente de la asíntota oblicua es 1, entonces: lím𝑥→+∞⁡𝑓(𝑥)𝑥=1⇔𝑎𝑒=1⇔𝑎=𝑒. Por simplicidad, supongamos que 𝑎 =𝑒 =1. De esta forma, la expresión de la función queda: 𝑓(𝑥)=𝑥2+𝑏𝑥2+𝑐𝑥+𝑑𝑥2+2𝑥+1.
    • Como 𝑓(0) =4, entonces 𝑑 =4.
    • Como la ordenada en el origen de la asíntota oblicua es 1, entonces: lím𝑥→+∞⁡(𝑓(𝑥)−𝑥)=1⇔lím𝑥→+∞⁡𝑥3+𝑏𝑥2+𝑐𝑥+𝑑−𝑥3−2𝑥2−𝑥𝑥2+2𝑥+1=1⇔𝑏−2=1⇔𝑏=3.
    • Como 𝑓(1) =34, entonces: 𝑓(1)=34⇔𝑐+84=34⇔𝑐+8=3⇔𝑐=−5.
    Por tanto, 𝑓(𝑥)=𝑥3+3𝑥2−5𝑥+4𝑥2+2𝑥+1.

Problema 5

Sean 𝑅 y 𝑄 las proyecciones ortogonales de un punto 𝑃 del plano sobre dos rectas fijas 𝑒1, 𝑒2 que forman un ángulo 𝛼.

  1. Determinar las ecuaciones del lugar geométrico que describe 𝑃 si el segmento 𝑅𝑄 es de longitud constante.
  2. Referir las ecuaciones del lugar a la referencia oblicua que definen las rectas 𝑒1, 𝑒2.
  3. Particularizar para el caso en el que 𝛼 =𝜋2.