Matemáticas de oposiciones

Siendo tg⁡(𝑧) =sen⁡(𝑧)cos⁡(𝑧), pruebe que para 𝑧 =𝑥 +𝑦𝑖 se cumple que tg⁡(𝑧)=sen⁡(2𝑥)+𝑖senh⁡(2𝑦)cos⁡(2𝑥)+cosh⁡(2𝑦),donde 𝑖=√−1.

La recta tangente a la parábola P de ecuación 𝑦2 =2𝑥 en uno de sus puntos 𝑃 ∈P corta al eje de ordenadas en el punto 𝐴 y la recta normal en 𝑃 corta a dicho eje en un punto 𝐵. Halle la ecuación del lugar geométrico que describe el baricentro del triángulo △𝑃𝐴𝐵 cuando el punto 𝑃 recorre P.

Considere la elipse de la figura. Determine en función de las longitudes 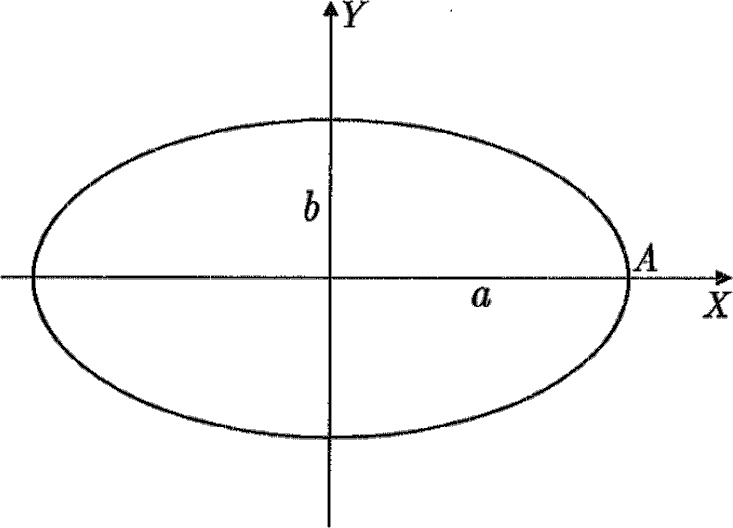𝑎 y 𝑏 de sus semiejes, un punto 𝑃 de dicha cónica situado en el primer cuadrante, tal que la superficie del cuadrilátero definido por las rectas tangentes a la cónica en 𝑃 y en 𝐴, y los semiejes coordenados positivos sea mínima.

En una circunferencia se escogen al azar tres puntos. Calcule la probabilidad de que los tres puntos estén situados en un mismo arco de 90 grados.

Calcule el valor del determinante ∣ ∣ ∣ ∣ ∣ ∣ ∣11!100⋯012!11!10⋯013!12!11!1⋯014!13!12!11!⋯0⋮⋮⋮⋮⋱⋮1𝑛!1(𝑛−1)!1(𝑛−2)!1(𝑛−3)!⋯11!∣ ∣ ∣ ∣ ∣ ∣ ∣.

Sean (𝑋,𝑌) una variable aleatoria bidimensional continua y la función 𝑓 :ℝ2 →ℝ definida como 𝑓(𝑥,𝑦)={𝑘(𝑦−𝑥),si 0≤𝑥≤𝑦≤2,0,en otro caso.

1. Determine el valor de 𝑘 para que 𝑓 sea función de densidad.
2. Halle la función de distribución asociada.